逻辑代数处理逻辑的基本方法是等效转换,而且只针对真值表、逻辑表达式、逻辑符号(图)三种表述方式。
1.真值表与逻辑表达式之间的等效转换
(1)最小项、真值表、标准与或表达式
1)最小项和真值表。
逻辑代数把包含全部变量(每个变量只以原变量或反变量形式出现一次)相与的“全变量乘积项”,叫做最小项。
用逻辑函数的全部变量的取值组合及其对应函数值排列成的真值表具有唯一性。
在真值表中,全部变量的每一种取值组合各对应一个最小项,其中对应0值的变量加反号、对应1值的变量不加反号。N个变量的逻辑函数有2N种取值组合,就有2N个最小项。最小项用m表示,并用变量取值组合对应的十进制数作为编号。表4-13~表4-15分别为二变量、三变量、四变量逻辑函数的真值表及最小项排布。
表4-13 二变量逻辑的真值表
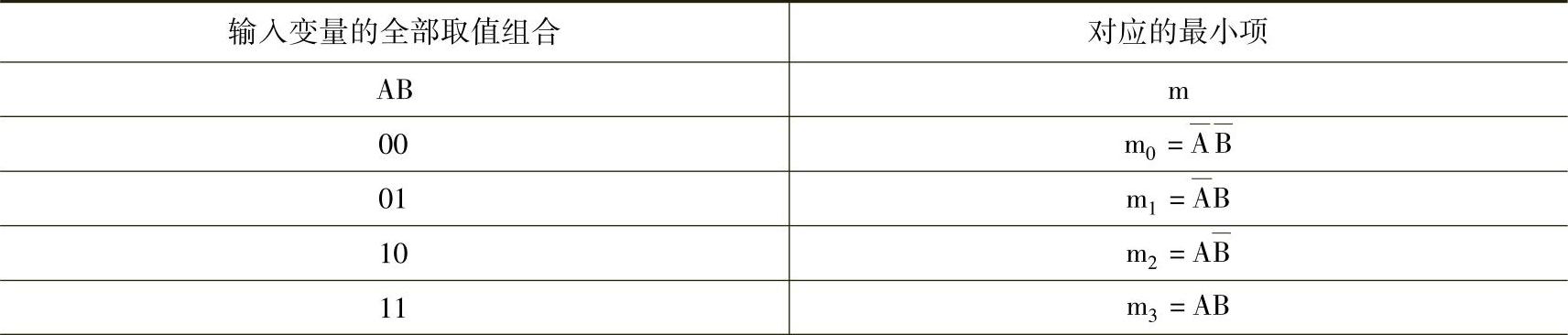
表4-14 三变量逻辑的真值表
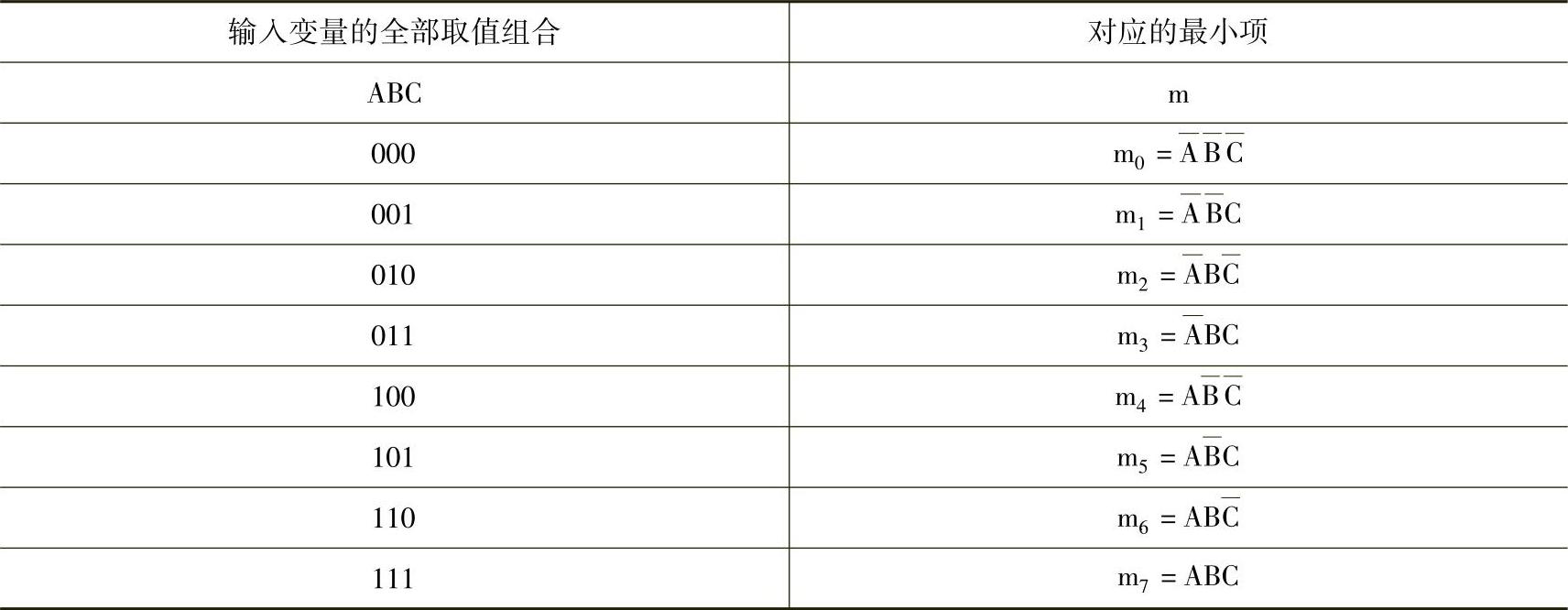
表4-15 四变量逻辑的真值表
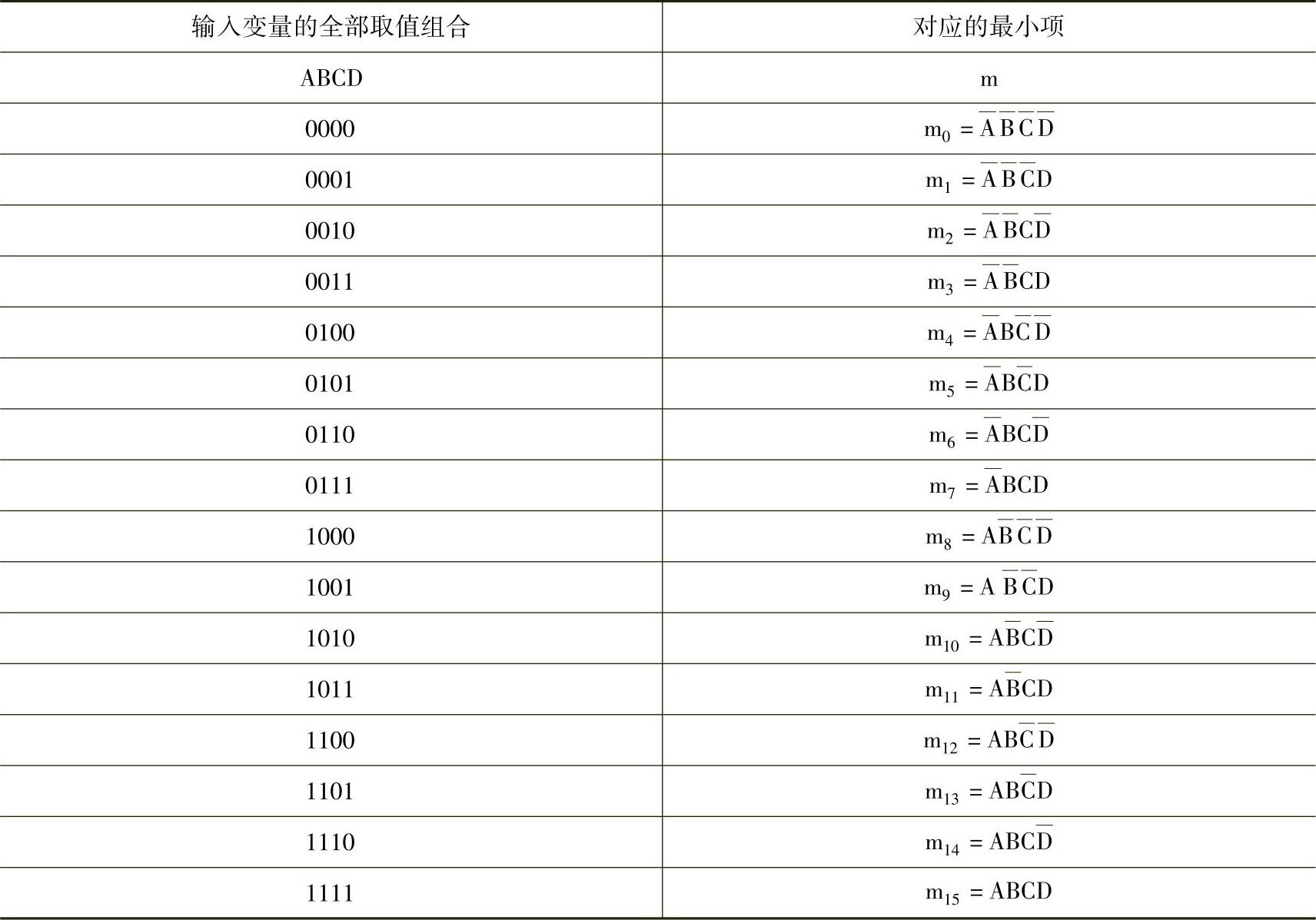
2)最小项和标准与或表达式。
由最小项相或构成的逻辑表达式叫做“标准与或表达式”,简称“标准与或式”。标准与或表达式的结构具有以下3个特点:
①式中只有与、或两种运算和对单变量取反的非号,无括号、无对运算取反的非号。
②式中与运算都是最小项,由对应同一种函数值(1或0)的全部且无重复的最小项组成。
③标准与或表达式具有唯一性。
(2)真值表与标准与或式的对应关系
前面介绍的基本逻辑表达式是依据基本逻辑的定义写出来的,方法没有普遍性。
由于标准与或表达式和真值表都具有唯一性,标准与或表达式的最小项与真值表中的变量取值组合有一一对应的关系,因此可确保两者转换的等效性。
1)按真值表写正函数的标准与或式。
在同一个真值表中,由函数取1值对应的最小项组成的标准与或式是逻辑正函数(也叫原函数)表达式。
以或逻辑的真值表(见表4-13)为例,按真值表写表达式的步骤如下:
①在真值表中找出使函数L=1所对应的变量组合及其对应的最小项见表4-16。
表4-16 或逻辑真值表及最小项

②最后把所有使L=1的最小项相或,得到的就是按真值表写出的标准与或表达式:
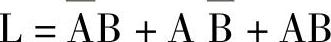
可用真值表(见表4-17)证明上式和或逻辑的定义式
L=A+B
是等效(相等)的。
表4-17 证明或逻辑的标准与或式与定义式等效真值表

通过实际数据运算证明两个表达式是等效的,即
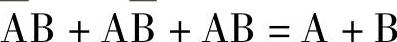
2)按真值表写反函数的标准与或式。
由真值表中函数取0值对应的最小项组成的标准与或式是逻辑反函数表达式。
把L=0的所有最小项相或,构成反函数的标准与或表达式。
表4-16的真值表中还有1组使L=0的组合:A=0、B=0,写成乘积项是
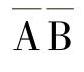
是A+B的反函数:
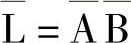
给正函数的表达式整体加反号也表示反函数:
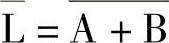
所以有
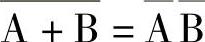
揭示正、反逻辑函数等效转换关系的就是下面将介绍的“摩根定理”。
3)标准与或式的另一种表述形式。
由于最小项在真值表中有确定的位置和编号,所以标准与或式都可用最小项求和的编号形式表示:
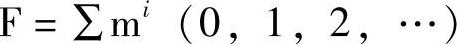
表达式中:Σ表示求和(即或运算),mi表示逻辑函数的最小项含i个变量,括号中的数字表示最小项的编号,如
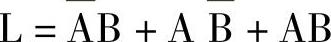
可以表示为
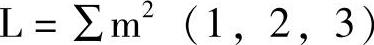
4)按表达式做真值表。
按表达式做真值表有计算法和最小项法两种常用方法。
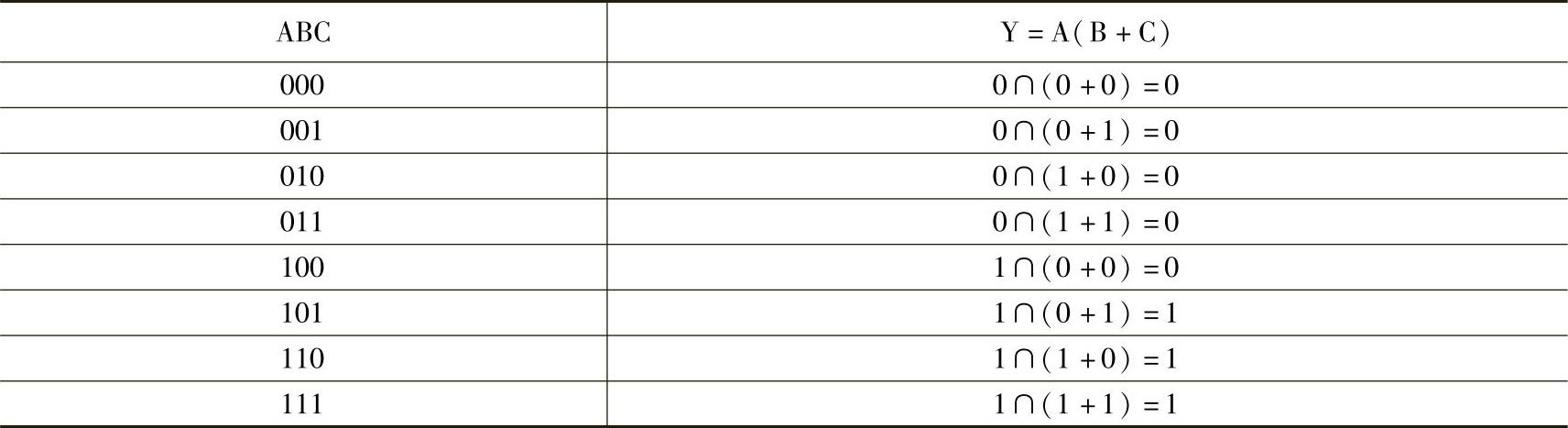
①计算法:将变量的各组取值分别代入表达式进行计算,把计算得到的函数值填入真值表的表格,就完成了逻辑函数真值表的制作,见表4-18。
表4-18 Y=A(B+C)的计算表
②最小项法:依据标准与或表达式跟真值表的对应关系,只要能得到逻辑函数的标准与或表达式,就可以做出逻辑函数的真值表,而任何形式的逻辑表达式都能转换为标准与或表达式。(https://www.daowen.com)
【例4-1】
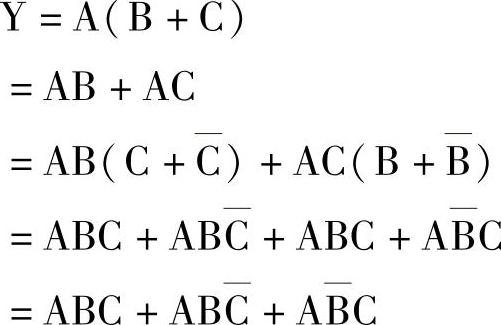
依据标准与或表达式中的最小项,按原变量对应1、反变量对应0的关系,可确定使函数取1值的变量组合(见表4-19)。
表4-19 最小项与取值组合的对应关系

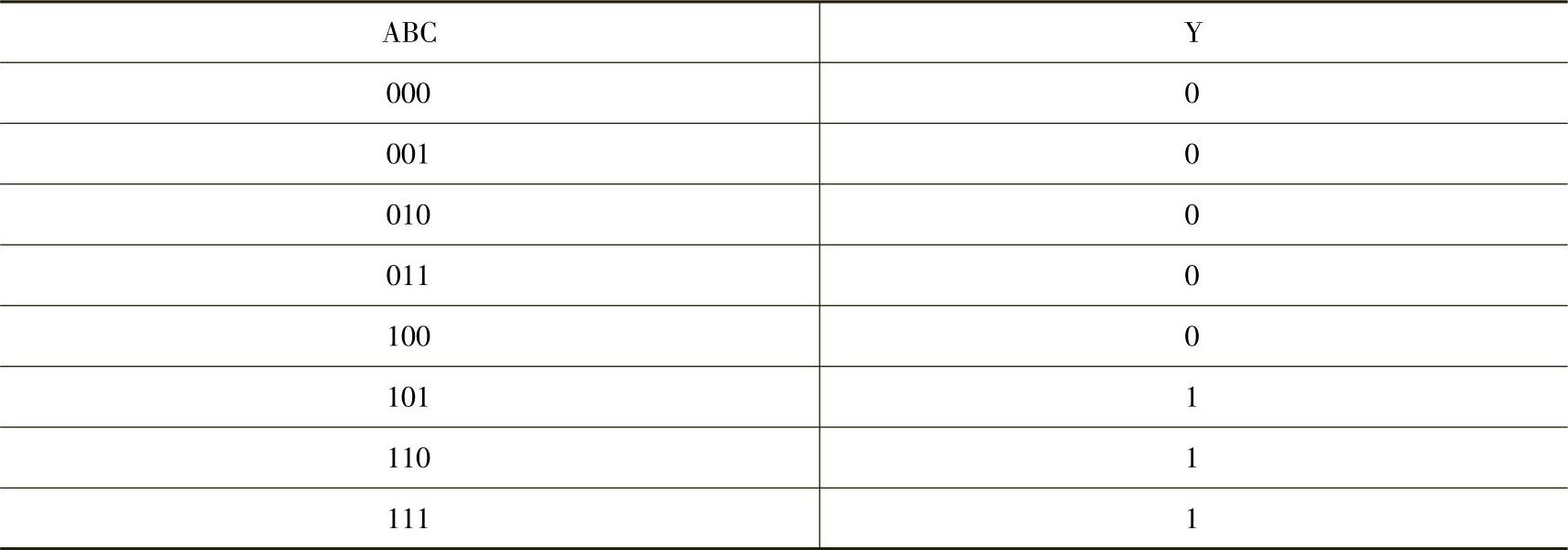
设计真值表,函数有3个变量A、B、C,全部变量的组合数为23=8种(N个变量的全部组合为2N种)。在变量取值组合对应的函数值位置填写1,其他位置填写0,做出的真值表见表4-20。
表4-20 Y=A(B+C)真值表
用计算法做真值表有时比变换标准与或式的方法简单。
2.表达式与逻辑图(符号)的等效转换
一个逻辑运算符对应一种逻辑门,一个逻辑表达式对应一个逻辑电路(图),逻辑运算顺序对应逻辑器件的连接关系。
(1)逻辑表达式与逻辑图的等效转换
1)基本逻辑运算顺序在逻辑图中的表示:逻辑运算顺序在逻辑图中体现为逻辑器件的连接顺序。
2)代入规则:在逻辑表达式中,任何变量都可以视作一个函数,而任何一个运算单元都可以用一个变量代换,如:
Y=AB+CD
若式中
D=MN+L
则有
Y=AB+C(MN+L)
如果又设
F=AB
表达式可变换为
Y=F+C(MN+L)
(2)按表达式画逻辑图
利用代入规则对表达式的运算顺序做分层处理,可保证按表达式画逻辑图的等效性。
按表达式画逻辑图的步骤:
1)确定变量个数,即逻辑图输入信号的个数。
2)借助代入法则对表达式的运算给予分层,直到变量为止,确定各层运算的逻辑符号。分层顺序:一般运算按或、异或、与、非、括号排序,多层的非运算按由上向下顺序逐层确定。
3)确定运算顺序,即逻辑图中逻辑符号的连接关系,画出逻辑图。
【例4-2】画出表达式
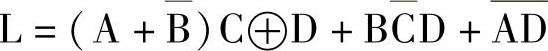
的逻辑图。
表达式中的变量:A、B、C、D,共4个。
对表达式的运算分层,确定各层运算需使用的逻辑符号,直到变量为止。
第1层(针对表达式整体):
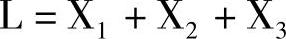
是3个输入信号的或运算(用三输入端的或门),其中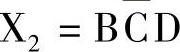 (是三输入端的与门,C信号要先经过非门),
(是三输入端的与门,C信号要先经过非门),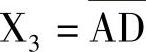 (是二输入与非门),而
(是二输入与非门),而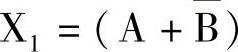 C⊕D还需要继续分层确定。
C⊕D还需要继续分层确定。
第2层(针对X1):
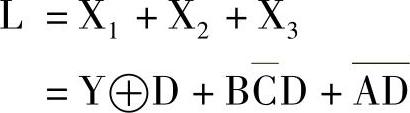
Y和D之间的运算用到一个异或门,而Y还需再分层。
第3层(针对Y):
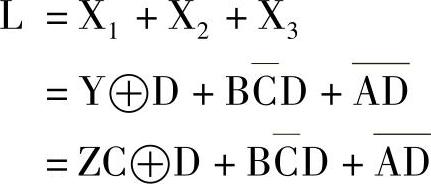
其中Z和C的运算用一个二输入与门。
第4层(针对Z):
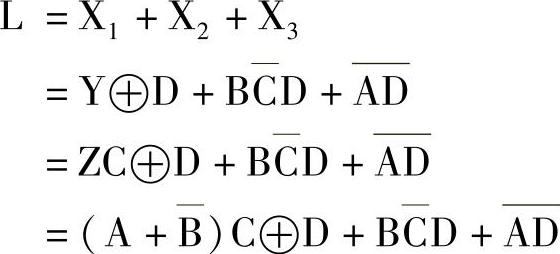
A、B之间的运算是二输入或门,其中B信号要先经过一个非门。
表达式中已全是变量,分层结束。最后,按表达式分层的逆顺序,用分析出的逻辑符号连接成逻辑图,如图4-9所示。
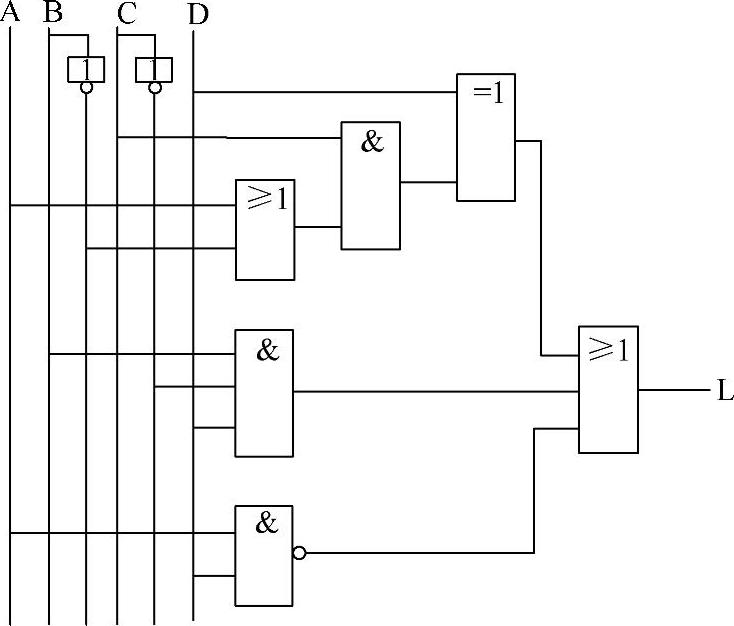
图4-9与L=(A+B)C⊕D+BCD+AD对应的逻辑图
(3)按逻辑图写表达式
1)由电路的输入端入手。由电路的输入端入手写逻辑表达式时,是从电路的输入端开始依次在各逻辑门的输出端写出它的运算结果,当写到电路的输出端时完整的逻辑表达式也就出来了。如图4-10所示就是这种方法。
电路的逻辑表达式为
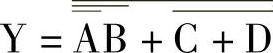
2)由电路的输出端入手。由电路的输出端入手写逻辑函数的表达式时,是先给电路中的各逻辑门的输入信号赋予一个临时代号,再从输出端入手依次把各个逻辑门表示的逻辑运算关系逐层代入,一直推写到输入端,完整的表达式就出来了。如图4-11所示就是这种方法。
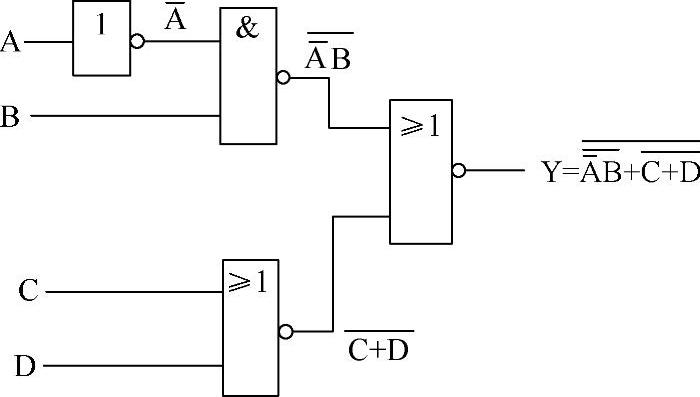
图4-10 由电路的输入端入手写逻辑表达式
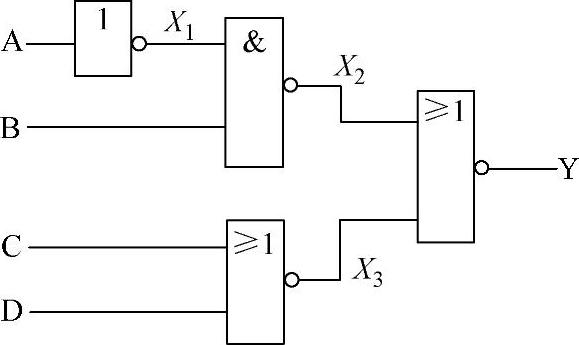
图4-11 由电路的输出端入手写逻辑表达式
电路的逻辑表达式为
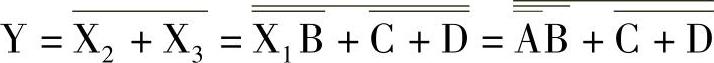
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





