放大器的输出信号幅度和相位都是随信号频率变化的，输出信号幅度与频率的对应关系称为放大器的幅频特性，输出信号相对输入信号的相位随频率的变化称为相频特性，两者合称为放大器频率响应特性，简称为频响特性或频率特性。影响放大器频响特性的主要是电路中的电抗元件和晶体管内部的结电容。

1.晶体管的高频等效模型

在高频电路中，晶体管两个PN结的结电容效应不能忽略。考虑结电容作用的晶体管等效电路模型称为晶体管高频等效模型（又称为混合π参数模型）。晶体管混合π参数模型的电路如图3-16所示。在晶体管的高频等效结构中，不能再用β值表示输出电流与输入电流的关系，改用跨导g_m表示。

在图3-16所示的等效电路中，r_ce>>R_L，r_ce可视为开路；相对高频信号，r_b′_c>>集电结电容C_μ的容抗，r_b′_c也可视为开路；与r_b′_c并联的发射结电容C_π对高频信号的衰减量会随信号频率升高而加大；C_μ直接把高频信号引到输出端，减小了高频信号在输入端的有效电流，与C_π的作用异曲同工，相当于给C_π并联一个小电容，可等效为一个电容C′_π。综合上述诸项原因，晶体管混合π参数模型可简化为如图3-17所示结构。

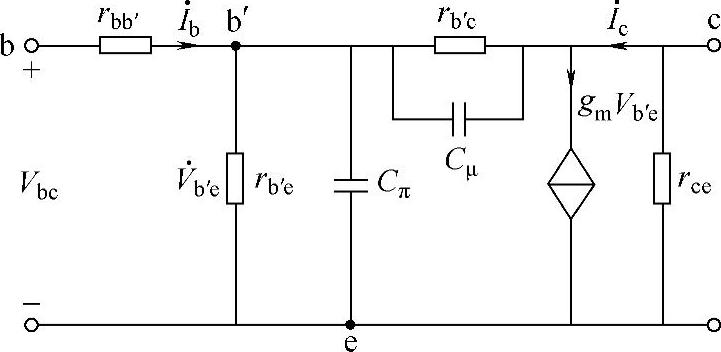
图3-16 晶体管的π参数等效电路结构

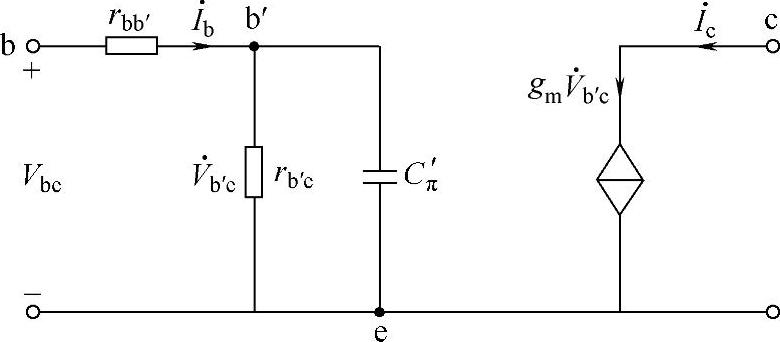
图3-17 简化的π参数等效电路结构

结电容C′_π对晶体管放大能力的影响表现为β值随信号频率的变化，如图3-18所示。

2.单管共发放大电路频响特性

单管共发放大电路的π参数等效电路如图3-19所示，晶体管外的电抗元件主要是耦合电容。出于表述需要，耦合电容C₁、C₂被保留。

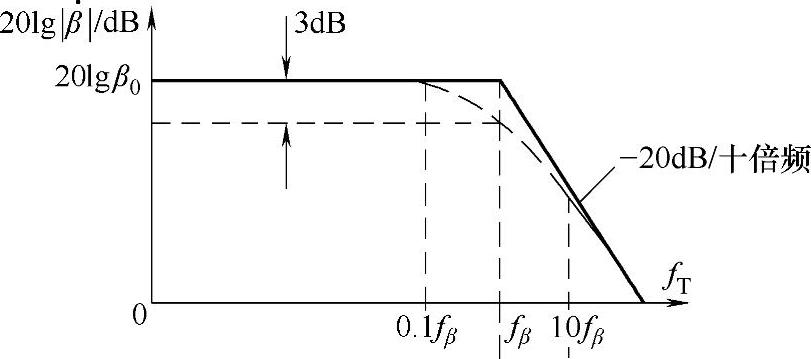
图3-18 β值随信号频率的变化曲线

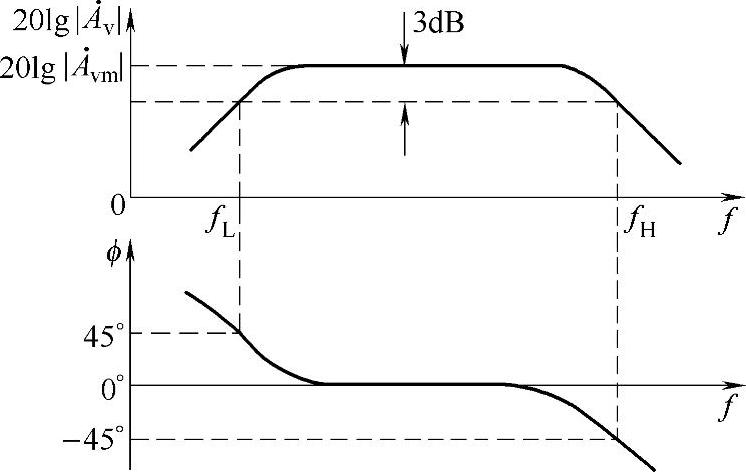
借助放大器的π参数等效结构，可对电路的频率特性做直观、定性的分析，即串联使用的输入、输出耦合电容（C₁、C₂）会衰减低频端信号，处于并联使用的等效结电容C′π衰减高频端信号，所以形成如图3-20上图所示的单管共发放大器的频响特性，中间平坦部分是放大器的通频带。

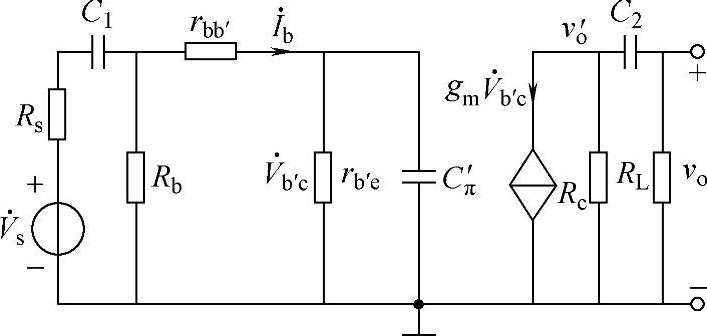
图3-19 单管共发放大电路的π参数等效电路

(www.daowen.com)

图3-20 单管共发放大电路的频响特性

耦合电容与结电容不但影响放大的频响特性，还影响输入、输出信号的相位关系，图3-20中下图为输入、输出信号相位关系随频率变化的特性曲线，称为相频特性曲线。

由于变压器通频带的最低频率由一次绕组电感确定，最高频率由变压器漏电感确定，所以变压器耦合的放大器通频带主要由变压器决定。耦合变压器的原绕组电感和整体漏电感要按放大器所需通频带设计制作。变压器铁心（或磁心）的磁滞损耗及磁路饱和会引起信号失真，也是需要注意的技术内容。

【边学边练】

用示波器测试模拟放大器

1．测试放大器的电压放大倍数A_v

把低频信号发生器的输出信号(＜50mV)接在晶体管放大器的输入端（图3-6中的A点），再用示波器CH1探头分别测出电路输入（A点）和输出（B点）的信号峰值（或峰一峰值），即可计算电路的电压放大倍数：

这里只是针对电路的输入、输出信号幅度进行比较、测算，与信号的相位无关。若用双踪示波器就可对A、B两点同时测试，并观察输出波形对输入信号的相位变化。

2．检测信号中的交直流分量

见表1—2，把⑩模式选择开关指向CH1，先把CH1探头脱离电路，并与接地夹短路。再把⑩CH1的输入耦合方式选择开关拨到DC位置。交直流叠加的信号是由直流电正负极性决定的单向信号，测试前需把0电压基线移到屏幕下方，并记住这个位置。把CH1的探头接到晶体管的集电极，即可看到交直流混合波形。实际只能看到交流波形．直流电压由扫描线的垂直移位体现，所以要记住测试前0电压基线的初始位置。

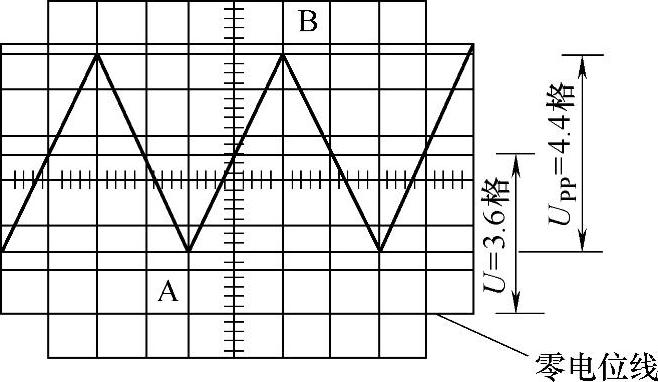
图3-21 交、直流电压合成波形

交、直流混合（又叫叠加）时交流总是浮在正电压的表面，如图3-21所示。

交、直流的幅度值等于直流与交流峰值之和，瞬时值等于交流信号瞬时值与直流之和，瞬时值表示方式见表3-1。