就是把定、转子之间的磁的耦合等效地变换成电路上的联系。

变换的方法和步骤是：

（1）首先用一个结构（相数、匝数、节距等）和定子绕组完全一样的假想绕组等效地代替短路绕组。等效的含义是，代替前后，各个环节消耗或传递的功率不变。

对假想绕组中的所有参数都附加“′”来表示，称为折算值（如E′₂，I′₂、r′₂、x′₂等），如图1-19所示。

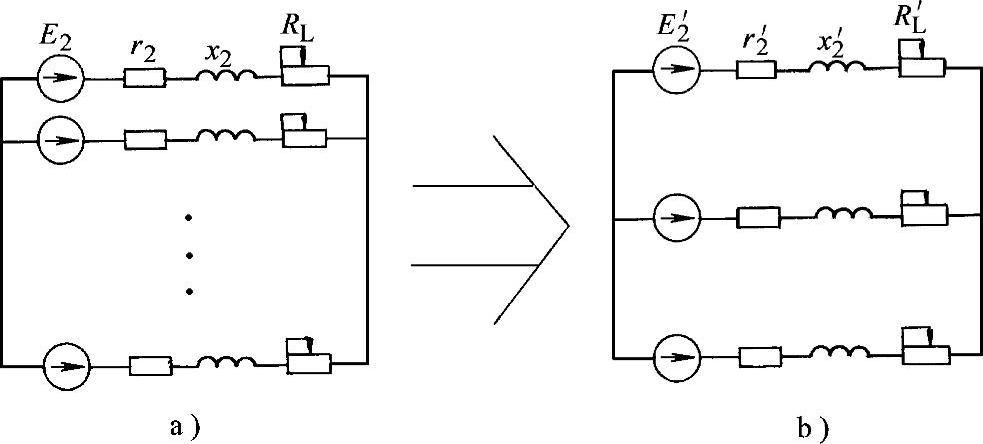
图1-19 短路绕组变换成假想绕组

a）静止短路绕组 b）静止假想绕组

满足等效条件的假想绕组各参数的计算方法（称为折算）如下：

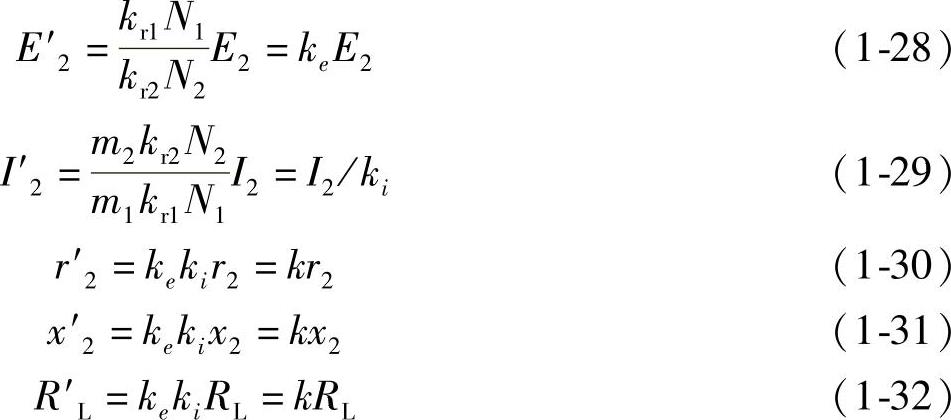
式中 k_r1、k_r2———定、转子绕组的绕组系数；

N₁、N₂———定、转子绕组的匝数；

k_e———电动势变换系数；

k_i———电流变换系数；

k———电动机的变比，k=k_ek_i。

用假想绕组代替短路绕组后得到的异步电动机的全电路如图1-20所示。图中：

r₁———每相定子绕组的电阻；

x₁———每相定子绕组的漏磁电抗；

I₁———定子侧的相电流；

E₁———每相定子绕组的反电动势。

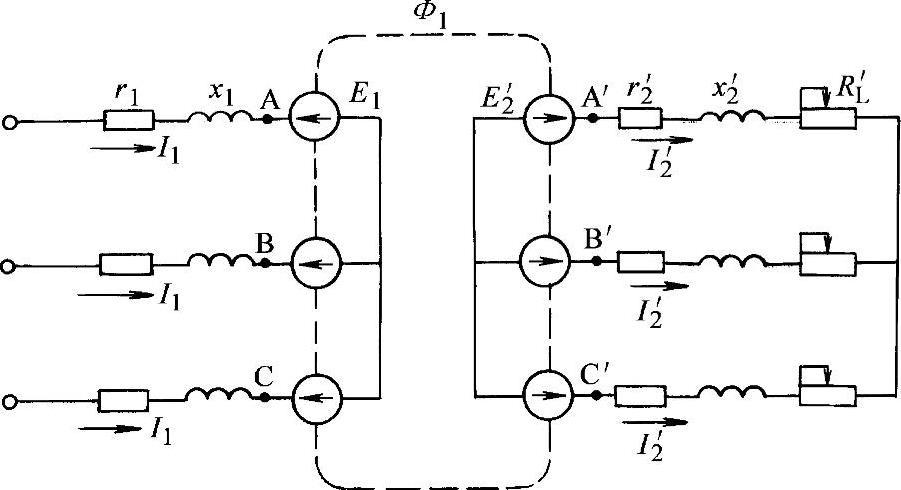
图1-20 假想异步电动机的全电路

在定子侧，电动势E₁是定子绕组切割旋转磁场的磁力线而产生的。在一定转速下，其大小反映了旋转磁场的强弱程度。它所吸取的电功率3E₁I₁本质上就是通过电磁感应传递到转子上的“电磁功率”P_M。

在转子侧，E′₂是静止“转子”的假想绕组切割旋转磁场的磁力线而产生的每相电动势。它标志着转子侧获得了能量，而电功率3E′₂I′₂就是转子侧通过电磁感应所得功率的大小。

（2）将定、转子电路直接相接。从以上叙述中，有两点值得注意：

1）如果忽略传递能量过程中的损耗，则有

E₁I₁≈E′₂I′₂

其含义是，由定子侧通过磁场传递的功率，已经全部被转子侧得到。

2）由于转子假想绕组的结构与定子绕组相同，两者又都切割着同一个旋转磁场，故

E₁=E′₂

从电路上看，定子侧的A、B、C三点间的电压与转子侧A′、B′、C′三点间的电压是一样的。

于是，如果将定子侧的A、B、C三点与转子侧的A′、B′、C′三点对应地联接起来（见图1-21），那么从能量传递的角度来看，图1-20和图1-21所示的电路是完全等效的。这样，就实现了用电路的联系来代替磁场的耦合了。

（3）因为异步电动机在运行时，三相电路总是平衡的，所以，通常只需画出一相的电路就可以了，如图1-22所示。

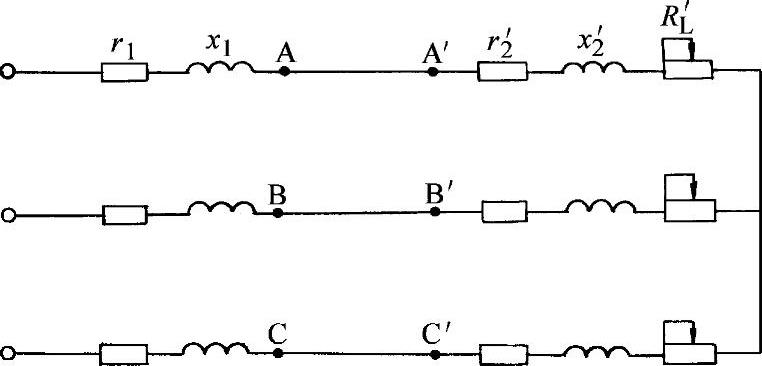
图1-21 由电的连接代替磁的耦合(www.daowen.com)

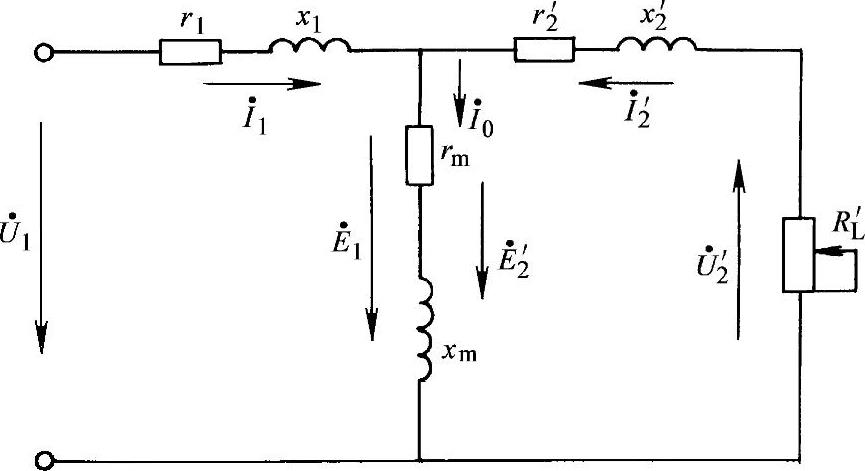
图1-22 一相等效电路

图中，r_m，x_m构成的支路称为励磁支路。对于励磁支路，可通过电动机在理想空载时的状态来说明。

所谓理想空载，就是绝对空载，也就是转子侧没有任何功率输出。在等效电路中的反映是n_M=n₀，Δn=0，s=0，R′_L=∞，I′₂=0，P_L=0。

在这种情况下的定子电流将仅仅用来建立磁场，故称为励磁电流，用I₀表示。

如忽略各项损耗不计，则这时的定子电路为一纯电感电路，如图1-23a所示。

由电工基础知识可知，在纯电感电路中，电源电压U₁是和自感电动势E₁（通常称为反电动势）相平衡的，即

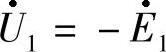
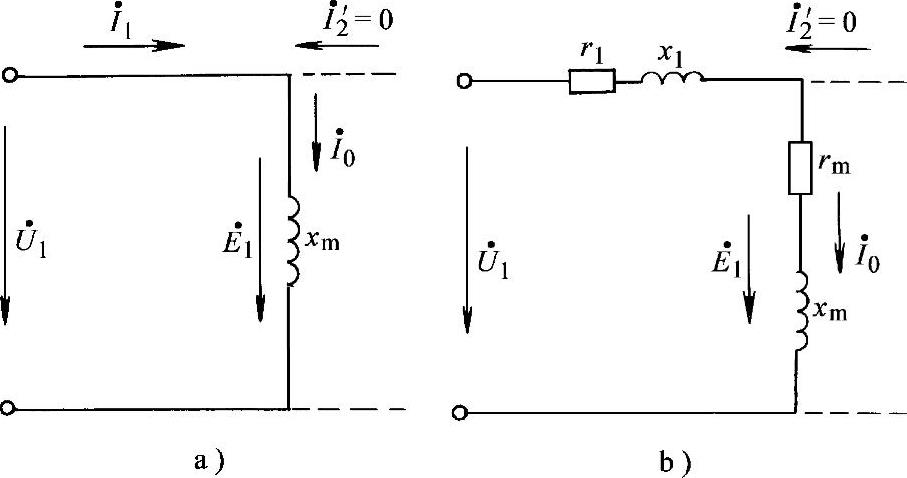
图1-23 理想空载时的等效电路

a）忽略各项损耗 b）计入各项损耗

而E₁在数值上等于电流I₀和感抗x_m的乘积，即

E₁=I₀x_m

所以，励磁支路在异步电动机中是用来建立主磁通的，在电路中以E₁=I₀x_m的形式来表现。

在以上的分析中，被忽略的因素有：

（1）定子绕组的电阻r₁，它将引起定子侧的铜损：p_Cu1=3I²₀r₁（p_Cu1是三相绕组的总铜损）。

（2）定子绕组的漏磁电抗。漏磁通是指少量的没有和转子绕组耦合的、未能起到传递能量作用的磁通，由它引起的感抗x₁，仅仅是增加了定子绕组的无功损耗3I²

0^x1。

以上两项都和定子电流I₁的大小有关，故不归到励磁支路中去。

（3）磁路中的铁损（磁滞损耗和涡流损耗），用等效电阻r_m来表示。因铁损主要和主磁通有关，故归入励磁支路中。

将上述因素计入后，就可得到图1-23b，再把转子部分接上，就是图1-22所示的作为分析异步电动机工况的主要工具的等效电路。

通过等效电路，容易得出异步电动机在运行过程中的关系式。

（1）定子侧的电动势平衡方程

式（1-33）表明，和电源电压相平衡的，除电动势E₁外，还有阻抗压降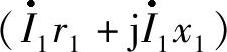。在频率为50Hz的情况下，后者所占比例很小，故U₁和E₁的有效值近似相等，即

U₁≈E₁

（2）电流方程（由磁动势的平衡方程导出）

式（1-34）表明，定子电流由两部分组成：小部分用于建立主磁通Φ_M（I₀）；大部分则提供给转子侧，使转子得到能量而拖动负载。

（3）转子的电动势方程

式中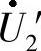———机械负载等效电阻R_L′两端的电压。乘积U₂′I₂′等于机械负载功率P_L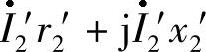；是转子侧的阻抗压降，所占比例很小。