牛顿法的基本思想是将目标函数f(X)在点X(k)处的泰勒展开式的二项式作为其近似函数式,然后求出这个近似函数的极小点作为原目标函数的近似极小点;若此值不满足精度要求,则以此近似极小点作为下一次迭代的初始点,继续以上过程,迭代下去,直至满足精度要求为止。
对于多元函数f(X),设X(k)为f(x)极小点X∗的一个近似点,在X(k)处将f(X)进行泰勒展开,保留到二项式得
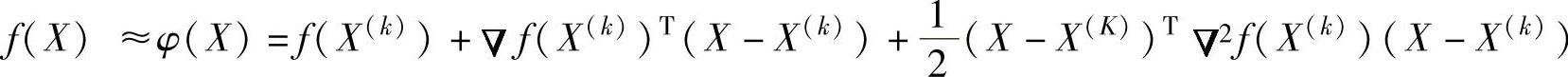
式中, 2f(X(k))为f(X)在X(k)处的海赛矩阵,下面记为G(X(k))。
2f(X(k))为f(X)在X(k)处的海赛矩阵,下面记为G(X(k))。
设X(k+1)为φ(X)的极小点,根据极值点必要条件可知
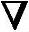 f(X(k+1))=0
f(X(k+1))=0
 f(X(k))+
f(X(k))+ 2f(X(k))(X(k+1)-X(k))=0
2f(X(k))(X(k+1)-X(k))=0
从而可以推出牛顿法的基本迭代公式为
X(k+1)-X(k)=-G(X(k))-1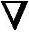 f(X(k)) (3-4)
f(X(k)) (3-4)
式中,G(X(k))-1为海赛矩阵的逆矩阵。
从牛顿法迭代公式的推演中可以看到,迭代点的位置是按照极值条件确定的,其中并未含有沿下降方向搜寻的概念。因此对于非二次函数,如果采用式(3-4)——牛顿法迭代公式,有时会使函数值上升,即出现f(X(k+1))>f(X(k))的现象。为此,需对上述牛顿法进行改进,引入数学规划法的搜寻概念,提出所谓“阻尼牛顿法”。
如果把
S(k)=-G(X(k))-1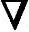 f(X(k))
f(X(k))
看作是一个搜索方向,称为牛顿方向,则阻尼牛顿法采用如下的迭代公式
X(k+1)=X(k)+α(k)S(k)=X(k)-α(k)G(X(k))-1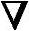 f(X(k))(k=0,1,2,…)
f(X(k))(k=0,1,2,…)
式中,α(k)为沿牛顿方向进行以一维搜索的最佳步长,可称为阻尼因子。
α(k)可通过如下极小化过程求得
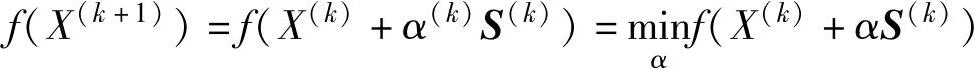 (https://www.daowen.com)
(https://www.daowen.com)
这样,原来的牛顿法就相当于阻尼牛顿法的步长因子α(k)取成固定值1的情况。由于阻尼牛顿法每次迭代都在牛顿方向上进行一维搜索,这就避免了迭代后函数值上升的现象,从而保持了牛顿法二次收敛的特性,而对初始点没有苛刻的要求。
阻尼牛顿法的计算步骤如下:
设f(X)二次可微,ε1、ε2为事先给定的小正数,X(0)为初始点,k=0。
1)计算矩阵 2f(X(k)),令Gk=
2f(X(k)),令Gk= 2f(X(k))。
2f(X(k))。
2)若Gk-1存在,且 f(X(k))TGk-1
f(X(k))TGk-1 f(X(k))>ε1,令S(k)=-Gk-1
f(X(k))>ε1,令S(k)=-Gk-1 f(X(k));否则,令S(k)=-
f(X(k));否则,令S(k)=-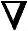 f(X(k))。
f(X(k))。
3)求解
minf(X(k)+αS(k))
s.t. α≥0
设αk是此一维搜索的最优解。
4)X(k+1)=X(k)+αS(k)。
5)检验是否满足终止准则(常取‖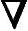 f(X(k+1))‖≤ε2)。
f(X(k+1))‖≤ε2)。
牛顿法应用于具有正定海赛矩阵的二次函数时,只需一次迭代即可达到无约束全局极小点。当初始点接近于极小点时,牛顿法产生的点列收敛于平稳点,且收敛速度是二阶。但是牛顿法每次迭代都要计算函数的二阶导数矩阵,并对该矩阵求逆矩阵,因此计算工作量很大,所占的计算机存储量也是很大的。
例3-5 设X(0)=(4 1)T,用牛顿法求解
minf(X)=1.5x21+2x1x2+x22-x1
解:根据条件可以求出
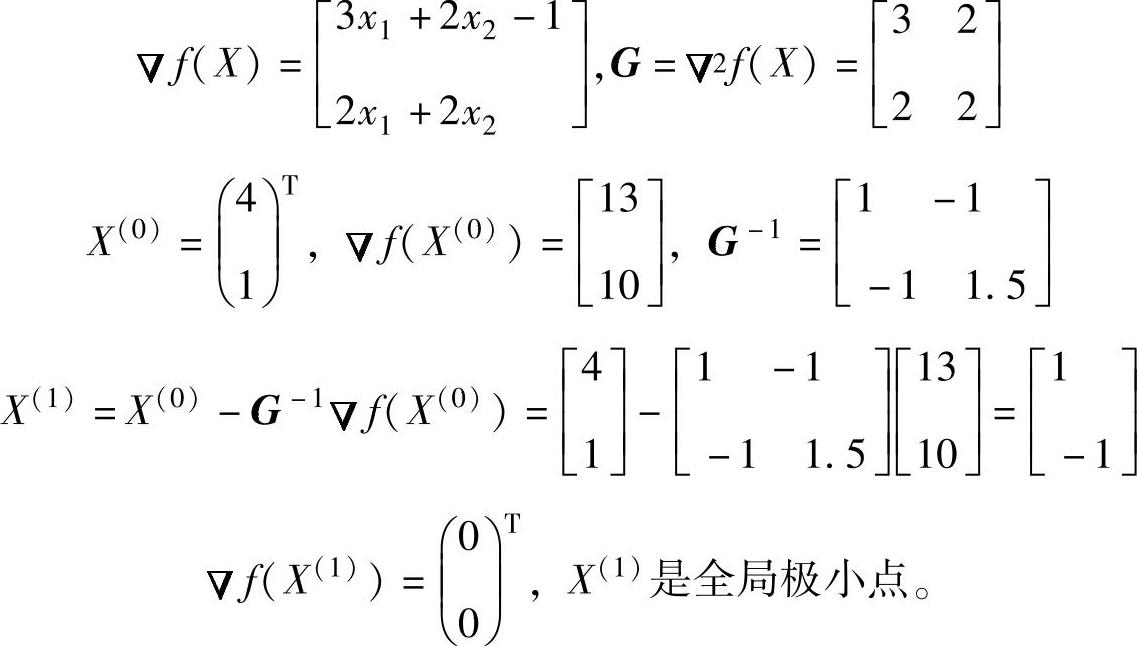
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





