无约束优化问题的极值条件是指使得目标函数取得极小值时，极值点所应满足的条件。对于可微一元函数f（x），在给定区间内某点x=x₀处取得极值的必要条件是

f′（x₀）=0

即函数的极值必须在驻点处取得，但是需要注意的是驻点未必都是函数的极值点。那么相类似的对于二元函数f（x₁，x₂），在点x₀（x₁₀，x₂₀）处取得极值的必要条件是

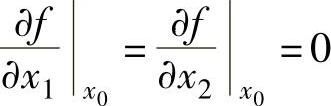
即梯度 f（x₀）=0

这个只是取得极值的必要条件，而要想建立极值的充分条件，则可以从二元函数的泰勒展开式进行推导证明，这里证明从略。

直接给出二元函数极值点的充分条件为：二元函数在该点处的海赛矩阵为正定，也就是要求海赛矩阵G（x₀）的各阶主子式均大于零，即

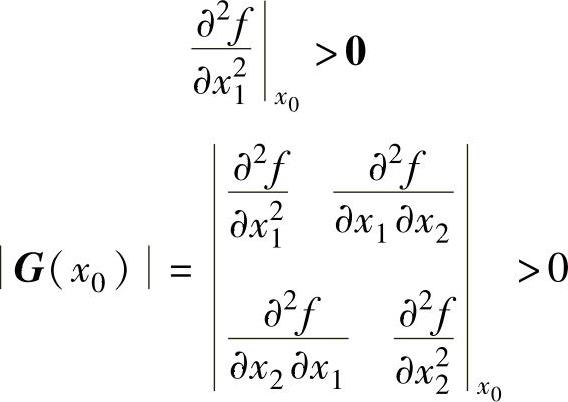
根据二元函数在x₀点取得极值的充分必要条件的推广，可以得到多元函数f（x₁，x₂，…，x_n）在x₀点取得极值的必要条件为函数梯度

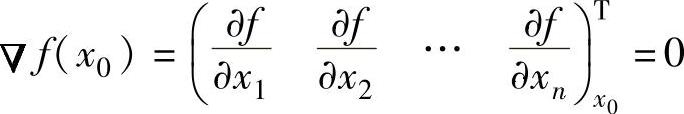
极值的充分条件为函数海赛矩阵

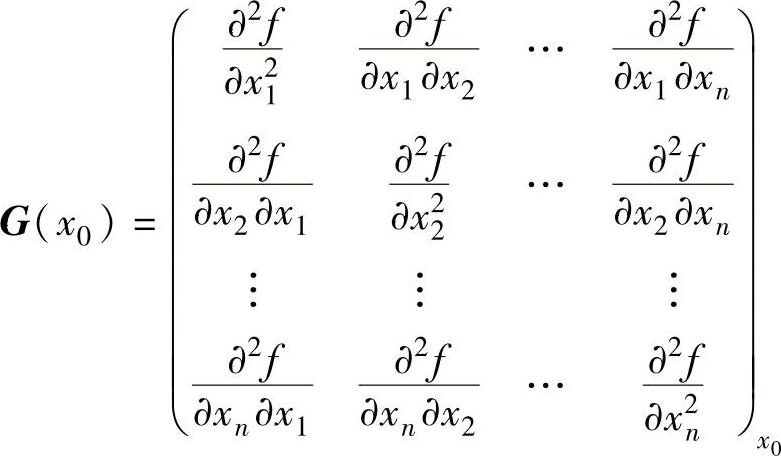(www.daowen.com)

正定，即要求G（x₀）的各项主子式均大于零。由于工程设计中，目标函数通常都比较复杂，海赛矩阵不易求得，它的正定性就更难判定了，所以一般说来，多元函数的极值条件在优化方法中仅具有理论意义。

例2-3 求下面函数的最优解

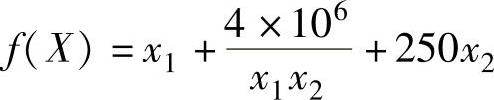
解：按最优解的必要条件

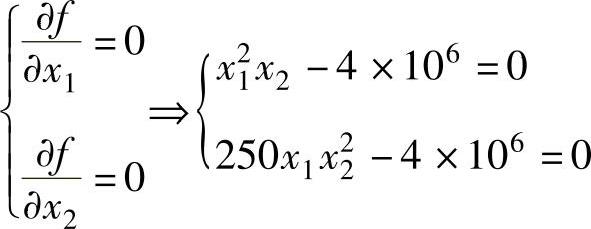
根据上面方程组可以求得，x₂^∗=4，x₁^∗=1000为满足必要条件的点。

再根据上面的方程组可以求得f（X）的海赛矩阵

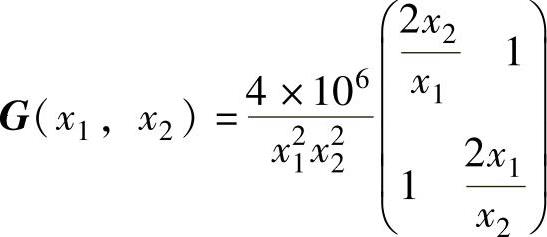
由于x₁、x₂均大于零，其海赛矩阵为正定矩阵。因此X^∗=（1000 4）^T是f（X）函数的局部极小点，由于海赛矩阵对于一切x₁＞0和x₂＞0均为正定，函数f（X）是凸函数，所以X^∗也是全域最小点，其f（X）函数的等值线图如图2-8所示。

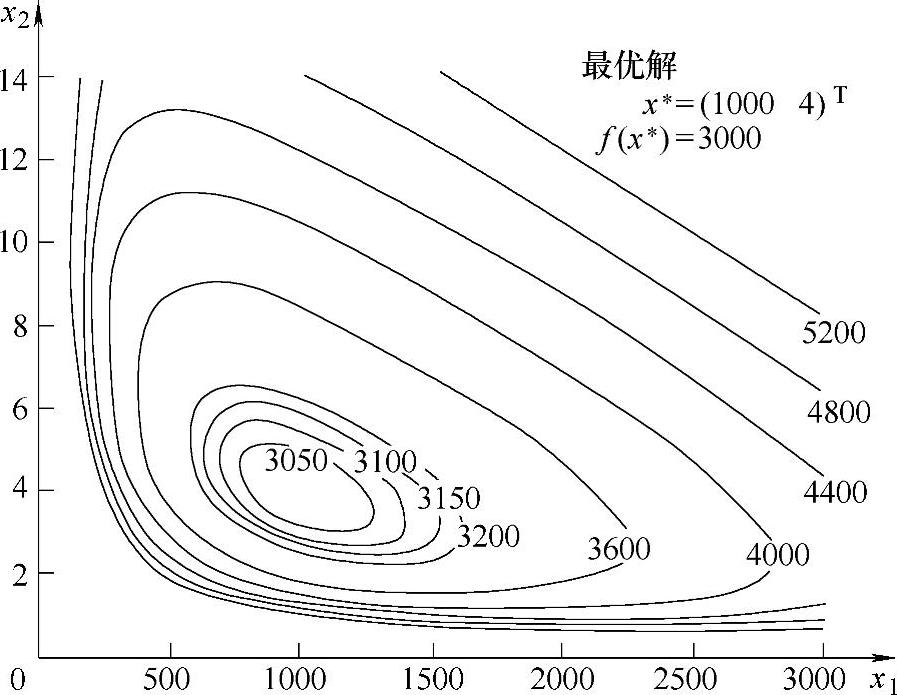
图2-8 函数的等值线图