优化问题一般是要求目标函数在整个可行域中取得最小点，即全局极小点。而根据函数极值条件所确定的极小点X∗，只是反映X∗附近局部性质，称为局部极小点。函数的局部极小点并不一定就是全局极小点（如一个函数有多个局部极小点时），只有函数具备某种性质时，两者才等同。这就需要进一步讨论局部极小点和全局极小点之间的关系，因而涉及凸集、凸函数、凸规划的问题。

1.凸集

一个点集（或区域），如果连接其中任意两点x₁和x₂的线段都全部包含在该集合内就称该点集为凸集，否则称非凸集，如图2-6所示。凸集的概念可以用数学的语言简练地表示为：如果对一切x₁∈R，x₂∈R及一切满足0≤a≤1的实数a，点ax₁+（1-a）x₂=y∈R，则称集合R为凸集。凸集既可以是有界的，也可以是无界的。n维空间中的r维子空间也是凸集（例如三维空间中的平面）。

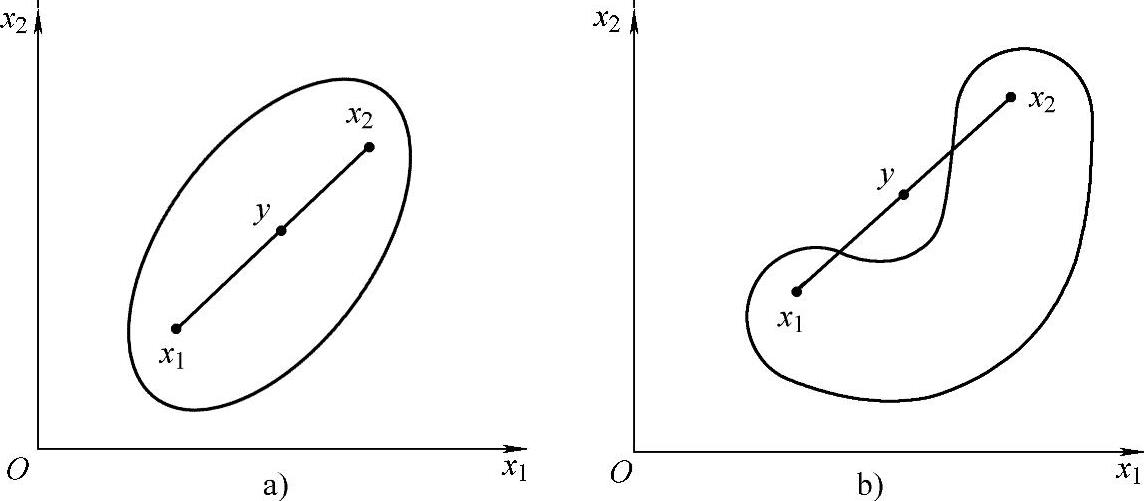
图2-6 凸集与非凸集

a）凸集 b）非凸集

2.凸函数及其判别条件

函数f（x），如果在其凸集定义域内任选两点x₁、x₂，恒有

f（αx₁+（1-α）x₂）≤αf（x₁）+（1-α）f（x₂）

式中，0≤α≤1，则称此函数为凸函数。如果上式去掉等号，则函数f（x）是严格凸函数。

凸函数的几何表现为，在其曲线上任意两点所连成的直线不会落在曲线弧线以下，如图2-7所示。(www.daowen.com)

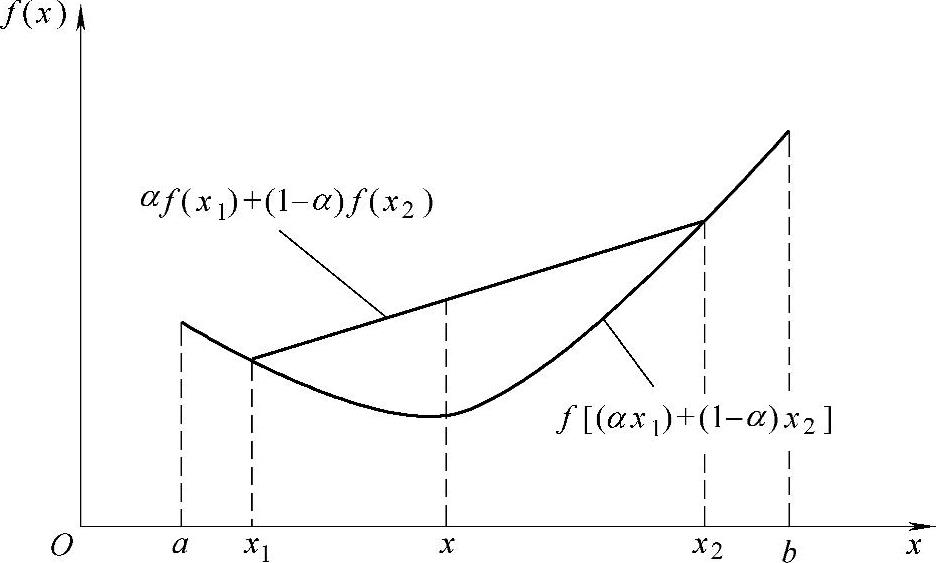
图2-7 凸函数的几何意义

凸函数的判别条件为：设f（X）为定义在凸集R上的具有连续二阶导数的函数，则f（X）在R上为凸函数的充分必要条件是海赛矩阵G（x）在R上处处半正定。

3.凸规划

对于约束优化问题

minf（X）

s.t.g_j（X）≤0（j=1，2，…，m）

若f（X）、g_j（X），j=1，2，…，m都为凸函数，则称此问题为凸规划。

可以证明，凸规划的可行域为凸集，其局部最优解即为全局最优解，而且其最优解的集合形成一个凸集。当凸规划的目标函数f（X）为严格凸函数时，如果其最优解存在，则最优解必定唯一。