图1-12　基尔霍夫电压定律

KCL是电荷守恒法则运用于集总参数电路的结果；KVL是能量守恒法则和电荷守恒法则运用于集总参数电路的结果。二者分别表明支路电流之间及支路电压之间的约束关系。这些约束关系与构成电路的元件性质无关，即无论是电阻、电容、电感还是电源，也无论是线性元件还是非线性元件，KCL、KVL只与电路的拓扑结构有关，而与支路特性无关。

电路中的节点和支路的数量之间存在一些关系，若电路的支路数是b，节点数是n，则：

（1）独立节点数是(n-1)。

（2）可列出(n-1)个独立的KCL方程。

（3）可列出L个独立的KVL方程，设L =b -(n-1)=b -n+1。

例1 - 4 图1 - 13所示电路有4个节点、6条支路，依次对a、b、c、d四个节点运用KCL可得：

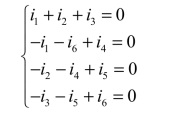(www.daowen.com)

将这4个方程相加，结果为0=0，说明方程组不独立，实际上任意舍去一个方程，余下的方程就是独立的了。

例1 - 5 图1 - 14中共有4个网孔，对各个网孔的回路依次运用KVL可得：

图1-13　例1-4图

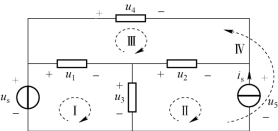
图1-14　例1-5图

同样地，将这4个方程相加，结果为0 = 0，说明方程组不独立。对于KVL来说，有几个网孔，就可以列几个KVL方程，去掉一个方程组就是独立的。