电荷守恒和能量守恒是自然界的基本法则,运用到集总参数电路中便得到基尔霍夫的两个定律。
基尔霍夫电流定律(Kirchhoff’s Current Law,KCL)表述为:任一时刻,电路的任一节点,流出该节点的所有支路电流代数和为零,即
![]()
其中,n0为该节点连接的支路数,ik为该节点的第k条支路的电流。上式即节点电流方程,简称KCL方程。
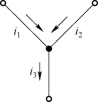
图1 - 9所示为集总参数电路中的一个节点,与该节点相连的各支路电流分别为i1、i2、i3,参考方向如图中所示。根据KCL,则有:
![]()
由上式可得
![]()
即
![]()
因此,KCL也可以表述为:在任一时刻,电路的任一节点,流入该节点的支路电流之和等于流出该节点的电流之和。
在以上的讨论中,对各支路的元件并无要求,这就是说,不论电路中的元件如何,只要是集总参数电路,KCL就总是成立的。
把KCL运用到节点时,根据各支路电流的参考方向,以流进为准或以流出为准来列写支路电流的关系式,两种标准可任选一种。
KCL反映了电路中节点相连的各支路电流间的约束关系,不仅适用于节点,还适用于包围几个节点的封闭曲面。如图1 - 10所示,根据KCL可得:
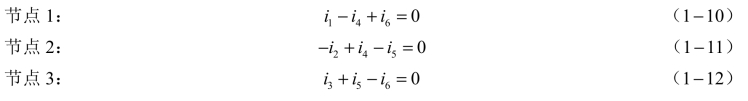
 (https://www.daowen.com)
(https://www.daowen.com)
图1-9 一个节点的支路
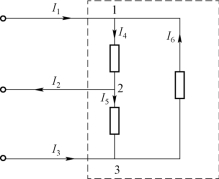
图1-10
以上三式相加,得:
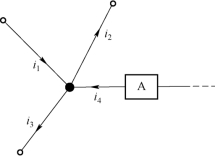
图1-11 例1-3图
![]()
可见,流入或流出一个封闭曲面的各支路电流的代数和恒为零,此即广义的KCL方程。
例1 - 3 在图1 - 11所示的某复杂电路的一个节点处,已知i1=5 A,i2=2 A,i3=-3 A,试求流过元件A的电流i4。
解 i1、i2、i3、i4是汇集于该节点的所有支路电流,满足KCL,线性相关,已知其中任何3个电流,即可确定另一电流。为此,必须先正确列出节点的KCL方程。设i4的参考方向如图中所示,由KCL得:
![]()
即
![]()
负号表示i4的实际方向与参考方向相反。
通过这个例1 - 3可看到,在运用KCL时常需和两套符号打交道。其一是方程中各项前的正、负号,其取决于电流参考方向与节点的相对关系;另一是电流数值本身的正、负号。两者不要混淆。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






