答：位移型圆锥配合是由内、外圆锥轴向位移（E_a）决定。

轴向位移（E_a）是指相互结合的内、外圆锥，从实际初始位置（P_a）到终止位置（P_f）移动的距离（图147）。

初始位置（P）是指在不施加力的情况下，相互结合的内、外圆锥表面接触时的轴向位置。而实际初始位置（P_a）则是指相互结合的内、外实际圆锥的初始位置（图147）。

终止位置（P_f）是指相互结合的内、外圆锥，为使其终止状态得到要求的间隙或过盈，所规定的相互轴向位置（图147）。

为控制实际初始位置的变动，位移型圆锥配合的内、外圆锥直径也应给出适当的公差。标准中推荐其直径公差带的基本偏差一般选用H、h、JS、js，其轴向位移的极限值按GB/T1801规定的极限间隙或极限过盈来计算。

由于相配合的内、外圆锥直径都给定公差，由此便产生极限初始位置，即初始位置允许的界限P₁和P₂，如图151所示。

极限初始位置P₁为内圆锥以最小极限圆锥，外圆锥以最大极限圆锥接触时的位置。

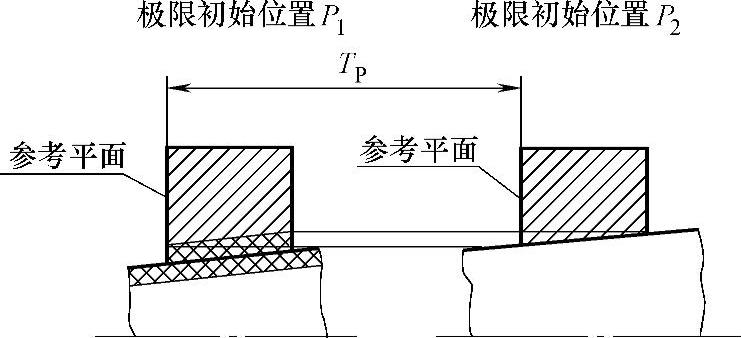
图151 极限初始位置

极限初始位置P₂为内圆锥以最大极限圆锥，外圆锥以最小极限圆锥接触时的位置。

由此可见，实际初始位置P_a便可控制在极限初始位置P₁和P₂之间。

初始位置公差T_P是指初始位置的变动量。它等于极限初始位置P₁和P₂之间的距离（图151）。

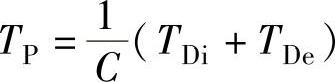
式中 C——锥度；

T_Di——内圆锥公差；

T_De——外圆锥公差。

如上所述，位移型圆锥配合是由内、外圆锥相对轴向位移来决定。当根据功能要求给出圆锥配合的性质（间隙配合或过盈配合）及配合极限值后，由此便可确定其极限轴向位移。

最小轴向位移E_amin是指在相互结合的内、外圆锥的终止位置上，得到最小间隙或最小过盈的位置。

最大轴向位移E_amax是指在相互结合的内、外圆锥的终止位置上，得到最大间隙或最大过盈的轴向位置。(www.daowen.com)

图152所示为在终止位置上得到最大最小过盈示例。

位移型圆锥配合的位移极限值（E_amin、E_amax）和轴向位移公差（T_E）按下列公式计算。

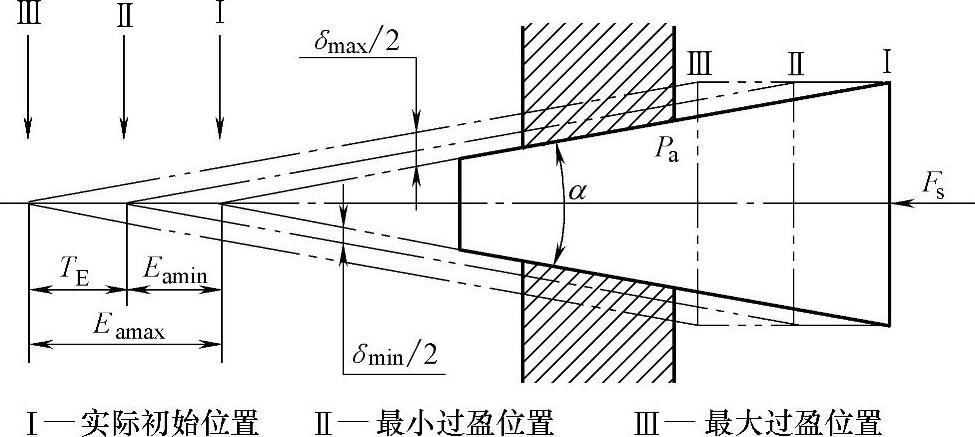
图152 位移型圆锥过盈配合

1）对于间隙配合

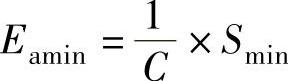
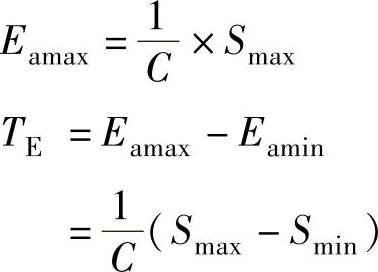
式中 C——锥度；

S_max——配合最大间隙量；

S_min——配合最小间隙量。

2）对于对盈配合

式中 C——锥度；

δ_max——配合最大过盈量；

δ_min——配合最小过盈量。

锥度过盈配合还可采取一定装配力来获取所需的过盈配合。

装配力（F_s）是指相互结合的内、外圆锥，为在终止位置（P_f）得到要求的过盈量所施加的轴向力（图152）。装配力大小需根据零件结构经机械设计计算取得。