答：由前述可知，在计算标准公差因子时，都是由公称尺寸来确定的。同样，在确定尺寸公差的许多参数中（如基本偏差等），也都与公称尺寸有关。

在生产中，零件的公称尺寸是各不相同的，若将每一种公称尺寸所对应的标准公差数值，一一对应地分别求出，所列出的公差表格就显得非常繁琐，使用也极不方便。从上述标准公差因子与公称尺寸之间的关系来看，相近数值的公称尺寸所求得的标准公差因子数值也极为相近，而且生产中也没有必要区分得过细。为了减少公差的数目，可统一公差值，以便于简化公差表格；方便生产中应用，标准中按一定规律将公称尺寸划分成若干范围段落，称为尺寸分段。

标准中公称尺寸分段所采用的方法是：对公称尺寸小于等于180mm的，采用不均匀递增系列；对公称尺寸大于180mm的，则采用优先数系R10与R20系列。具体分段方法见表2。

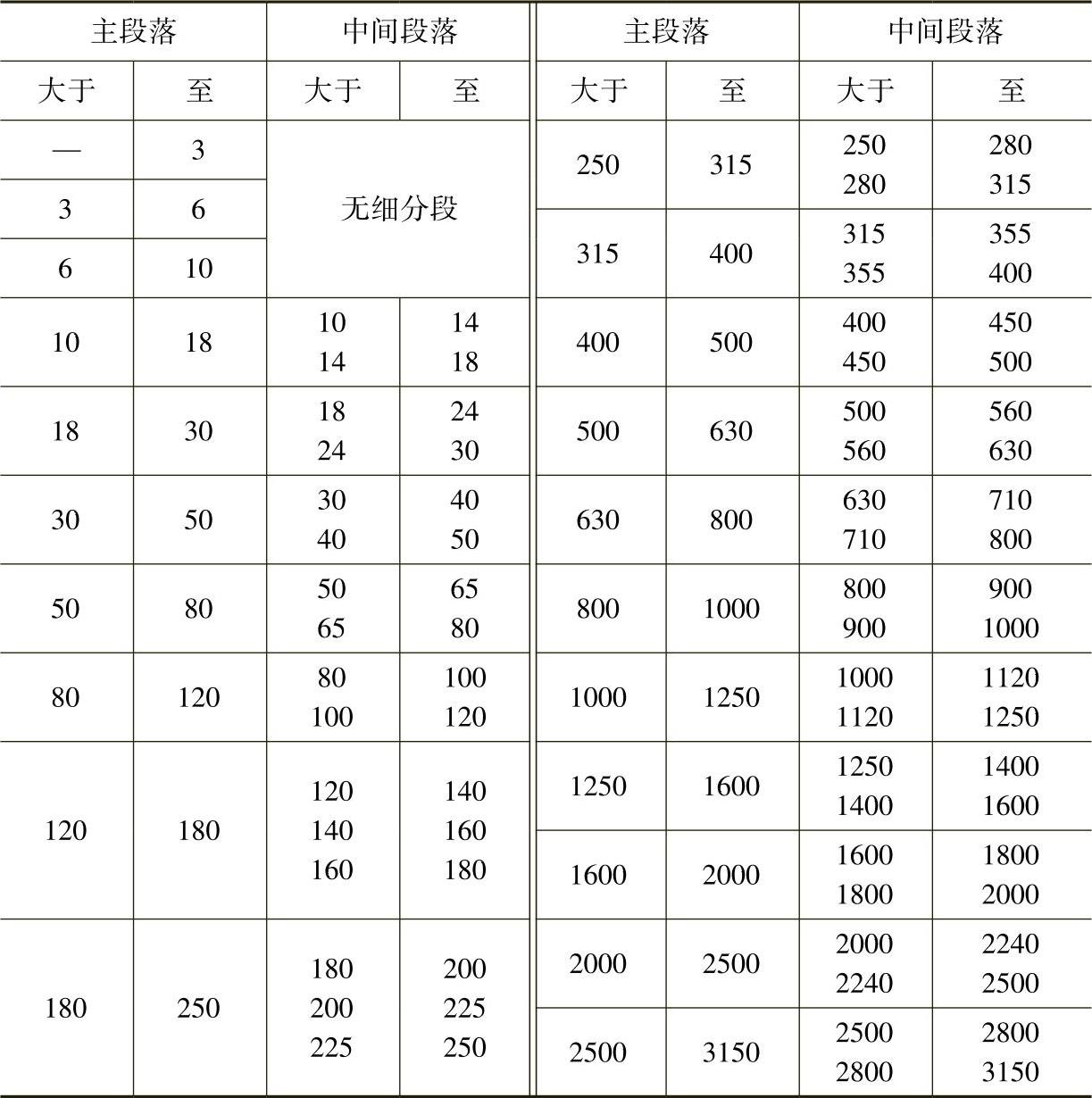
表中公称尺寸分段分为主段落和中间段落两部分。其中中间段落仅用于计算尺寸至500mm的轴的基本偏差a～c及r～zc或孔的基本偏差A～C及R～ZC和计算尺寸大于500～3150mm的轴的基本偏差r～u及孔的基本偏差R～U。

表2 公称尺寸分段 （单位：mm）

在计算各公称尺寸段的标准公差和基本偏差时，式中的D用每一尺寸段中首尾两个尺寸（D₁和D₂）的几何平均值，即

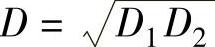(www.daowen.com)

例 计算大于30～50mm公称尺寸段的标准公差因子。

首先确定大于30～50mm公称尺寸分段计算值

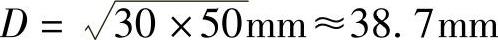
然后代入题29所给出的标准公差因子计算公式中，便可求得该尺寸分段的标准公差因子

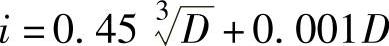
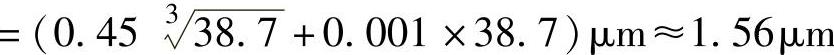
对于小于或等于3mm尺寸段的公称尺寸分段值，则用1mm和3mm的几何平均值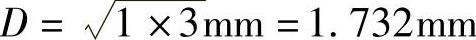来计算标准公差和基本偏差。