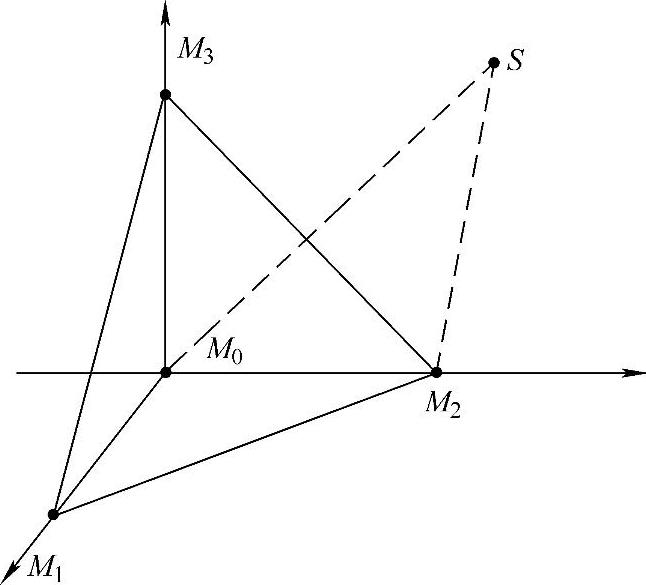
图6-16 直角四面体阵列

时间延迟，简称时延，是指声源信号到达麦克风阵列中不同阵元的距离差而引起的传播时间差。根据语音信号处理的理论和方法，利用时延可以估计出声源的方位角和空间位置等相关参数。

时延估计根据目标声源和检测系统的不同，可以分为以下两种。

（1）主动时间延迟估计 最常见的主动时延估计系统的应用包括雷达和声纳等，主动时延估计系统可通过主动发出探测信号来搜寻被测目标。当声波遇到被测目标后就会反射回到主动时延估计系统，然后该系统可以根据信号发出和探测目标后信号返回的时间差，结合时间差和麦克风阵列的几何模型就可以计算出目标声源信号的方位角等信息。

（2）被动时间延迟估计 被动时间延迟估计系统，顾名思义，是指被动的通过麦克风等传感器接收目标声源信号，而不需要主动发出电磁波或声波去探测目标。然后再根据发出的时间和返回的时间计算出时间延迟。在本书所提及的时延均为典型的被动时间延迟估计。

近些年来，随着人们对基于时延的声源定位算法的关注和研究，很多优秀的时延估计算法被研究出来了。其中，用得比较多的有传统互相关函数（NCC）、广义互相关函数（GCC）、自适应时延估计算法（LMS）等。优秀的时延估计算法应具有复杂度低、鲁棒性强和实时性高等特点。

1.互相关算法求时延

常用的测量两个突发型声发射波之间时差的技术不适用于连续型声发射源，而互相关技术既适用于断续波之间的时差或时间延迟测量，也适用于连续波之间的时差，或时间延迟测量任意一个波A（t）和另一个延迟时间为τ的波B（t+τ）之间的互相关函数（CCF）（图6-17），由式（6-49）给出：

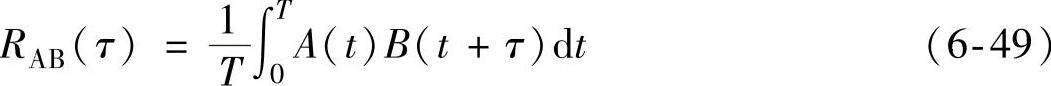
式中，T为一个有限的时间间隔。

从式（6-49）可见，如果τ是变化的，则互相关函数是τ的函数。R_AB（τ）的特性可以通过将A（t）和B（t）分为n个小的相等时间段的积来观察。令t=t_i，A（t）=a_i，B（t）=b_i，i=0，1，2，…，n。如果B（t）相对于A（t）有一时间延迟τ′，则

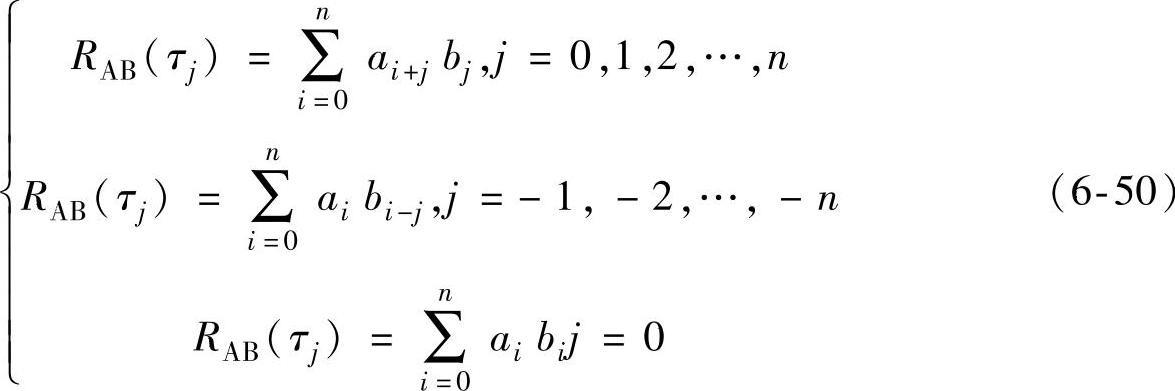
方程组（6-50）中a_i+j和b_i-j中下标随R_AB（τ_j）中τ_j的变化而变化。

互相关函数是在有限时间范围内的积分。在实际应用中，数据采样仅利用了每个波的有限部分，而在被利用部分之外的波幅为零，即如果i＞n，a_i=b_i=0；如果j＞0且i+j＞n，则a_i+j=0；如果j＜0且i-j＞n，则b_i-j=0。因此，当j增加时，i+j增加，方程组（6-50）中的某些求和项将为零。随着j的增加，求和项数将越来越少，R_AB（τ_j）的幅值逐渐下降。最终，当j＞n，所有a_i+j和b_i-j项为零，R_AB（τ_j）。当τ_j=τ′时，由于A和B为同相位，则R_AB（τ_j）达到最大值。因此，从R_AB（τ_j）的最大峰值部位可以获得B（t）相对于A（t）的时差或时间延迟τ′。

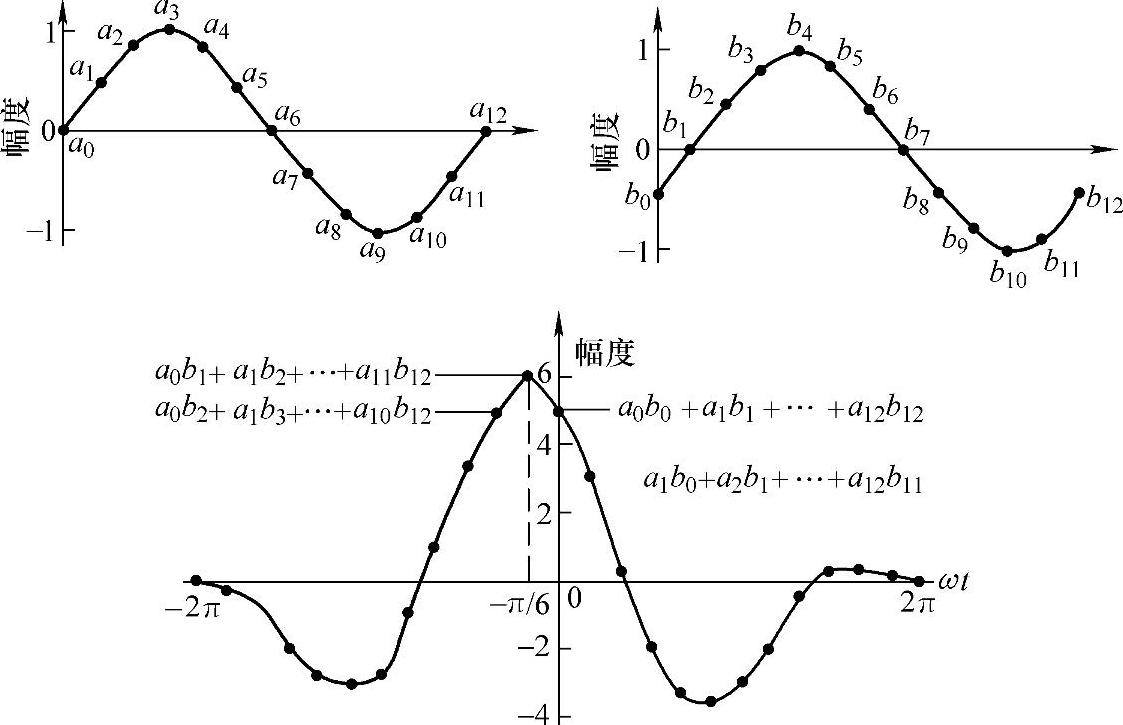
图6-17 互相关函数求解示意图

对于任意一函数A（t）和时间延迟为τ′的函数B（t），两个函数A（t）和B（t+τ′）在有限时间间隔内的互相关函数R_AB（τ_j）在τ=τ′时肯定包含一个最大值，这一互相关方法可用于连续型声发射源的定位。通常可以应用双通道快速傅里叶（FFT）变换分析来实现互相关函数分析。从频域v中互相关谱G_AB（v）的逆傅里叶变换可以得到时域τ中的互相关函数R_AB（τ）

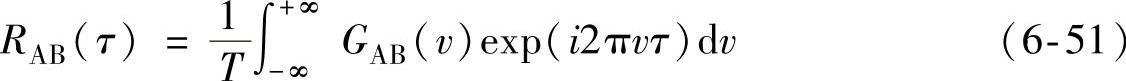
式中，G_AB（v）为A（t）和B（t+τ）的傅里叶变换。

2.广义互相关函数法(www.daowen.com)

在试验中由于噪声与混响的存在会使得互相关函数峰值不明显或存在多个峰值。为了锐化峰值，可以先对信号进行滤波处理，这等效于在频域的加权处理，有利于加强接收信号中源信号的谱分量，提高信噪比，从而获得更高的时延估计精度（图6-18）。

图6-18 广义互相关函数解算流程

H₁、H₂为滤波函数，则x₁（n）、x₂（n）经滤波后的互功率谱函数为

G₁₂（ω）′=H₁H₂^∗G₁₂（ω） （6-52）

H₂^∗为H₂的共轭函数。此时经滤波处理后的x₁（n）、x₂（n）信号的广义互相关函数可以表示为

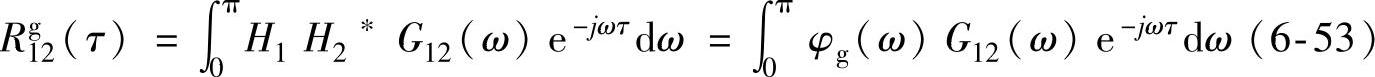
式中，φ_g（ω）为广义互相关加权函数，等效于给信号一个滤波效果。

广义互相关法通过求两信号之间的互功率谱，并在频域内给予一定的加权，来对信号和噪声进行白化处理；增强信号中信噪比较高的频率成分，从而抑制噪声的影响；再反变换到时域，得到两信号之间的广义互相关（GCC）函数。

常用的加权函数有CC、Roth、SCOT、PHAT四种，它们的定义与特性列于下表。加权函数要考虑不同的噪声与混响情况有针对性地选取使R^g₁₂（τ）的峰值得到锐化，也是实现准确时延估计的一个难点。

表6-2 几种常见的加权函数

3.自适应时延估计法

首先需了解自适应滤波器的原理。自适应滤波器是一种不需要事先了解输入信号的特性，在工作过程中能自动调节本身参数的“智能”滤波器。LMS自适应时延估计（Least-Mean-Square Time Delay Estimate）则是自适应滤波器的应用。实质上是在接收信号前加一时延，通过调整时延，使得信号经过LMS算法后与理想信号达到最大相关，起到自适应信道均衡的作用。其原理图如图6-19所示。

通过模拟两路信号，一路是另一路的回波，并且有700点的时延（图6-20）。为了考验该时延估计的性能，将两路信号的噪声的均值和方差都设计得不一样。进行滤波器的权重更新时，采用梯度法进行LMS的实现。当迭代次数较大时，即hm（n）稳定时，可以通过观察hm（n）的最大的m值来确定时延。根据时延滤波器的形状，取到最大值的时候就是延迟的点数。

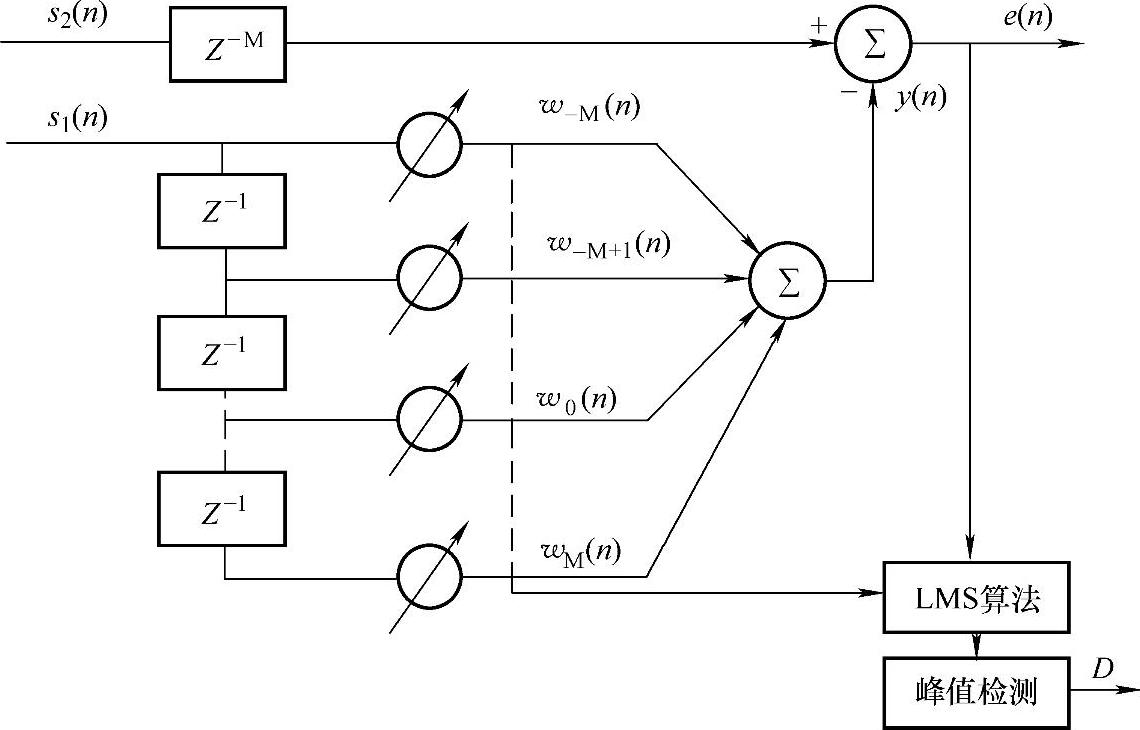
图6-19 自适应滤波器原理图

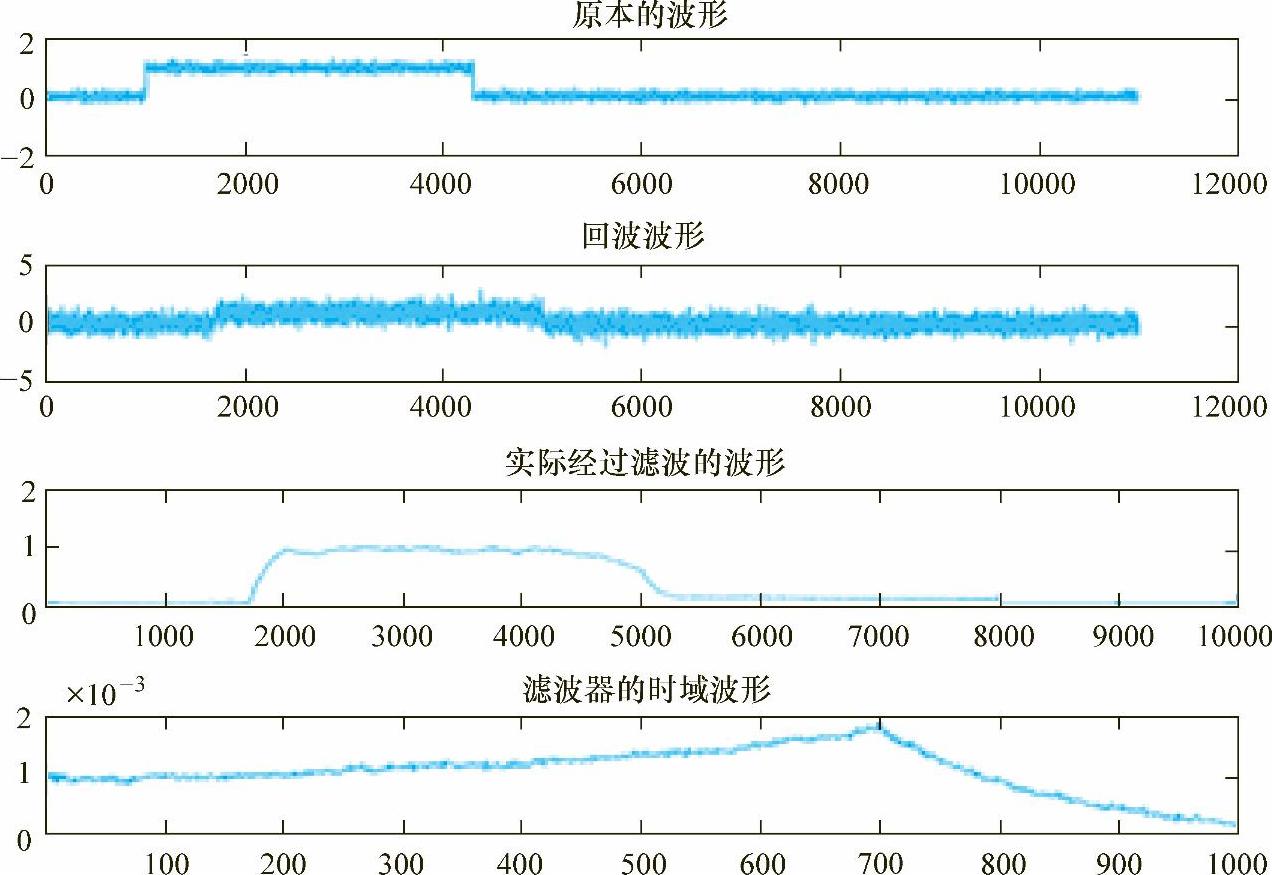
图6-20 自适应滤波模拟图