机电复合传动系统不同工作模式间的选择与切换由驾驶员的不同操作以及整车的控制系统来决定，并通过操纵元件（离合器或制动器）的接合或分离来实现。我们可以把车辆的每种工作模式看作一种状态，这些状态间的切换可以看作由一系列离散事件造成。同时，在每种特定工作模式下，可以把此时的车辆动态子系统看作一个相对独立的连续变量动态系统。

因此，机电复合传动系统可以描述为连续时间动态系统和一系列离散事件动态系统及其相互作用的切换系统。在进行机电复合传动系统控制系统设计时，必须详细建立模式切换前后离散状态与切换过程中连续状态的切换系统模型，这里定义为机电复合传动系统的复杂模型，为后文进行模式切换动态特性分析和控制策略研究奠定必要基础。

8.2.2.1　离散事件动态系统

以EVT1模式切换到EVT2模式为例，按照上文设定的操纵时序，模式切换过程需要经历EVT1模式、离合器C1接合阶段、制动器BK分离阶段以及EVT2模式，如图8.3所示。

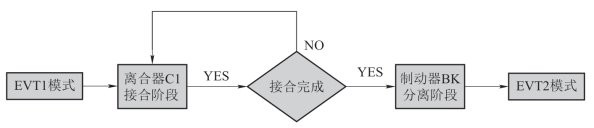
图8.3　模式切换过程操纵元件时序

由此可见，模式切换过程被划分为四个阶段，每个阶段对应不同的离散状态，各状态之间的系统结构和动态特性各不相同。结合上式，集合I为离散状态的有限集合，主要用于描述车辆的不同工作状态，因此离散状态集合I可表示为

式中，离散状态i1表示EVT1模式；离散状态i2表示离合器接合阶段；离散状态i3表示制动器分离阶段；离散状态i4表示EVT2模式。

离散事件集E可表示为

式中，离散事件e1=（i1，i2）表示从EVT1模式切换到离合器接合阶段；离散事件 e2=（i2，i3）表示从离合器接合阶段切换到制动器分离阶段；离散事件e3=（i3，i4）表示从制动器分离阶段切换到EVT2模式。

8.2.2.2　连续变量动态系统

连续变量动态系统主要描述车辆在不同转矩作用下的转速变化规律，模式切换过程的四个不同阶段分别用动力学方程来表示。

（1）EVT1模式：离合器C1断开，制动器BK锁止。

（2）离合器C1接合阶段：离合器C1处于接合状态，制动器BK锁止。

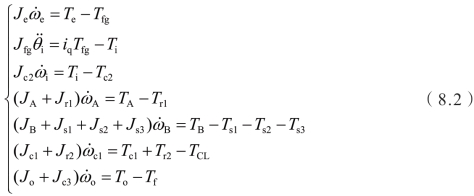
（3）制动器BK分离阶段：离合器C1锁止，制动器BK处于分离状态。

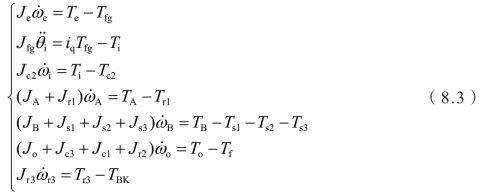
（4）EVT2模式：离合器C1锁止，制动器BK断开。(www.daowen.com)

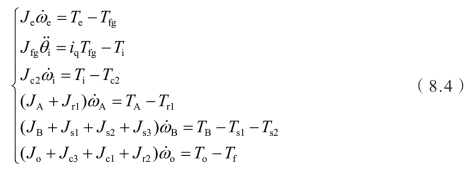
对应的状态变量集合和控制变量集合的选择如下所示：

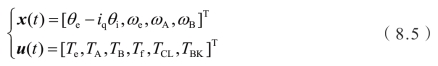
由于模式切换过程具有不同的工作模式，当选择不同时，微分方程的描述形式也不一样，状态映射函数 fi体现着离散系统的决策结果对连续受控过程动态行为的支配作用，即离散状态ik与连续变量动态子系统的映射关系为

式中，Ak为状态变量矩阵；Bk为控制变量矩阵，具体表达式详见附录。

8.2.2.3　模式切换规则

切换规则的设计关键在于规范与离散事件相对应的连续状态集合的逻辑约束条件，用以表征连续时间动态系统对离散事件动态系统的映射关系。针对本章的研究内容，关键在于设计出机电复合传动系统在模式切换过程中发生状态切换的临界条件。模式切换控制流程如图8.4所示。

从图8.4可以看出，从EVT1模式切换到EVT2模式过程发生的离散事件依次为 e1=（i1，i2），e2=（i2，i3），e3=（i3，i4）。结合第2章所设计的模式切换规律与本章所提出的切换系统概念，模式切换过程可描述为：当车辆行驶在低速工况时，系统处于EVT1模式；当车速大于换挡车速v12时，电机对离合器进行调速，使得离合器两端速差小于阈值ωc，触发离散事件e1=（i1，i2），系统进入离合器接合阶段；当离合器两端速差等于0时，离合器锁止，触发离散事件 e2=（i2，i3），系统进入制动器分离阶段；当制动器两端速差大于阈值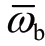时，制动器断开，系统进入EVT2模式。

离合器C1和制动器BK在接合或分离过程中的速差公式如下：

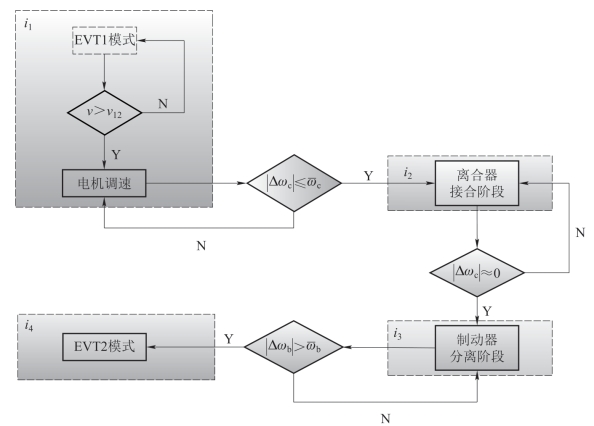
图8.4　模式切换控制流程

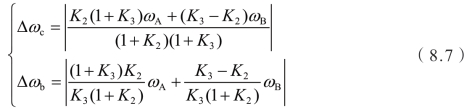
假设切换信号σ是一个逐段常数函数，它可以依赖于时间、它本身的过去值、系统的状态量、输出量或者系统的外部信号等。参照模式切换过程控制流程，机电复合传动系统的模式切换规则如下：

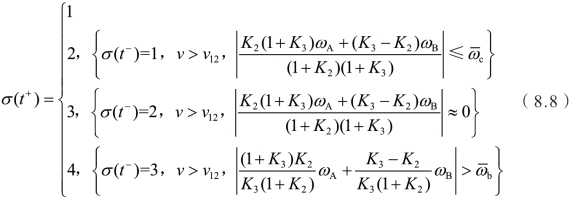
综合以上研究，通过引入切换系统的概念，将机电复合传动系统转化为一个集离散事件动态系统和连续变量动态系统及其相互作用为一体的切换系统，基于切换系统的机电复合传动系统复杂模型如图8.5所示。

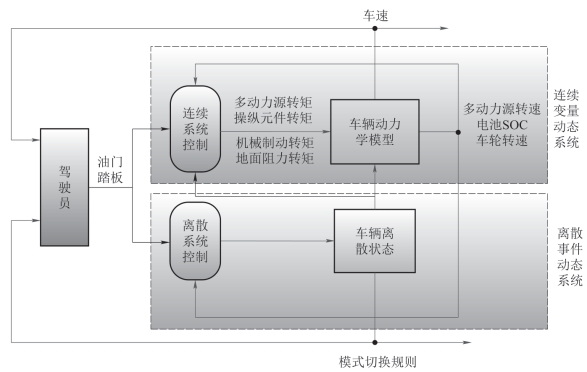
图8.5　基于切换系统的机电复合传动系统复杂模型

8.2.2.4　模式切换规则与模式切换规律的关系

分析图8.4、公式8.8与第5章中图5.2和图5.10，可以发现，本节在切换系统概念下所提出的模式切换规则是在模式切换规律的基础上，进一步细化了离合器和制动器的接合与分离过程。由于能量管理策略是机电复合传动系统的关键技术，发动机、电机工作点以及工作模式均应当由能量管理策略给出，从这一角度出发，模式切换规则可认为是能量管理策略的一部分；此外，模式切换规则在每个控制输入时刻，选择是继续以当前模式工作，还是切换到其他模式，实际上对应一个瞬时决策过程，更加适合嵌入瞬态控制策略构架中，因此可将模式切换规则嵌入后文所提的模式切换控制策略中以验证规则的效果。