1.串行进位加法器

在第1章我们通过例1.2.2研究过一位全加器，并得到一位全加器的电路符号（图3.1.3）。将n个一位全加器串联起来就得到n位串行进位加法器，如图3.2.16所示。

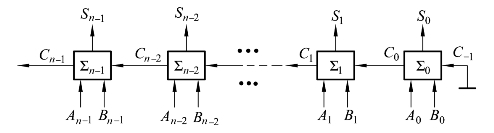
图3.2.16　n位串行进位加法器

显然串行进位加法器是逐级进位的，当最高进位Cn－1产生后才完成运算。设TTL基本门延时为Δt，因为

这种与非-与非式由两级与非门实现，所以一位全加器的进位延时为2Δt。那么一个16位串行进位加法器的进位总延时为32Δt。

2.并行进位加法器*

为了提高运算速度，在单片机中通常采用并行进位加法器。令di=AiBi为生成函数，ti=Ai+Bi为传递函数，则Ci=di+tiCi－1。

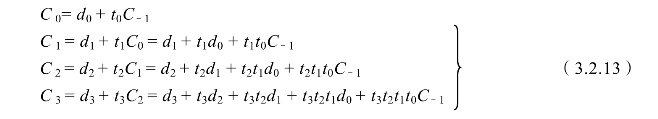
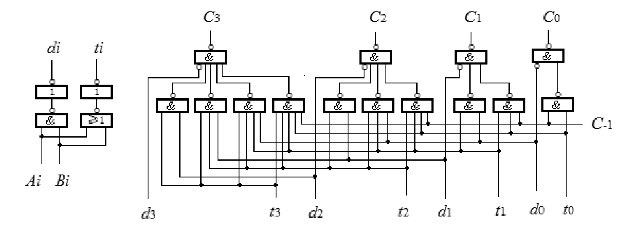
图3.2.17　四位并行进位链

（3.2.13）式称为并行进位链，对应电路如图3.2.17所示。因为，所以生成函数和传递函数的产生需要2Δt的延时。另外，（3.2.13）式的C0～C3均可化为与非-与非式，所以当生成函数和传递函数产生后，只需2Δt的延时即可同时产生C0～C3。

但是受门电路扇入系数（≤8）的限制，对于16位加法器不能按（3.2.13）式继续做下去，只能每4位分为一组，形成4组。将（3.2.13）式的最高进位定义为C3=D0+T0C－1，其中D0=d3+t3d2+t3t2d1+t3t2t1d0为组间生成函数，T0=t3t2t1t0为组间传递函数。

同理组间进位遵循逻辑关系Ci=Di+TiCi－1，按（3.2.13）式的方法可组成组间并行进位链：

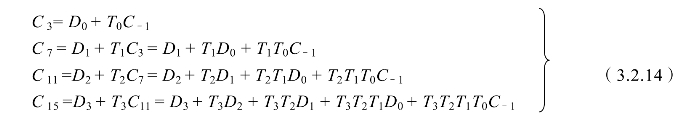
从（3.2.13）和（3.2.14）式可知，16位并行进位加法器的生成函数和传递函数的产生需要2Δt的延时，组内并行进位需要2Δt的延时，组间并行进位需要2Δt的延时，所以16位并行进位加法器的总延时只需6Δt延时。这个延时不到16位串行进位加法器延时的1/5。

【例3.2.4】用8421BCD码表示十进制数，试设计两位十进制加法器。

解：两位十进制加法器需要8位二进制加法器。用8421BCD码表示的两个1位的十进制数进行相加，若其和出现伪码（即大于9）或者该位向高位产生了进位，则该位的和还要加6进行修正。由此列十进制数进位的逻辑真值表，如表3.2.5所示。

表3.2.5　十进制数进位的真值表(www.daowen.com)

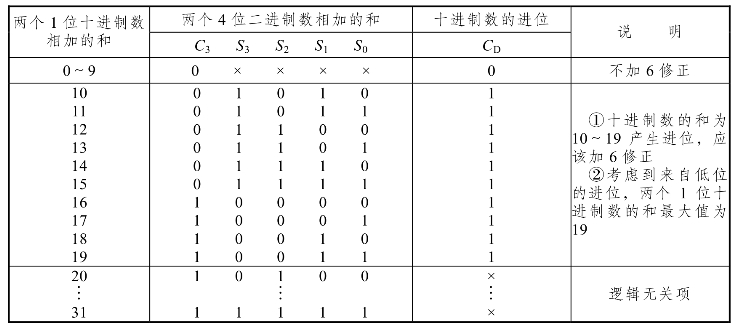
由真值表得CD的卡诺图，如图3.2.18所示。由卡诺图得十进制数进位CD的逻辑函数

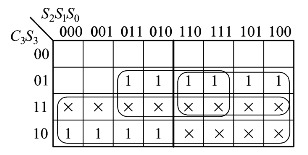
图3.2.18　CD的卡诺图

根据图3.2.16和式（3.2.15）得两位十进制加法器电路，如图3.2.19所示。

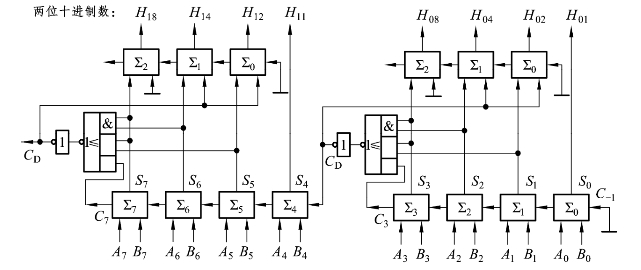
图3.2.19　两位十进制加法器电路

【阅读】补码加法器*

在单片机内部是不会集成例3.2.4那样的电路来实现十进制运算的，十进制运算是通过编程实现的。即十进制运算以8421BCD码为运算对象，进行二进制运算，最后对结果给予修正。总之所有的算术运算都是以补码加法器为核心，即使乘、除法运算电路也如此。

1.补码加减法的算法

2.补码的加减法运算电路

根据（3.2.16）式，单片机（MCU）的算术逻辑单元ALU将加减法运算统一为同一个电路来实现。如图3.2.20所示。当控制信号M=0时电路实现[X+Y]补的运算；当控制信号M=1时电路实现[X－Y]补的运算，其中[－Y]补等于[Y]补按位取反（包括符号位）后末位加1。

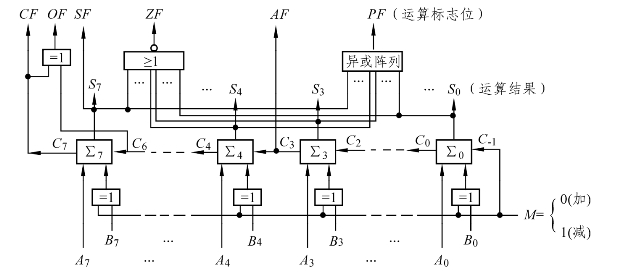
图3.2.20　八位补码加减法运算电路

3.运算标志位

在单片机的ALU中还要设置一些运算结果的标志位，如进位标志CF、溢出标志OF、符号标志SF、零标志ZF、辅助进位标志AF、奇标志PF等。这些标志位为1表示运算结果具有某种特征，提供给汇编语言程序员做出正确的判定和处理，因为数据是由编程者定义的。若针对无符号数运算，编程者关注的是CF；若针对有符号数（补码）运算，编程者关注的是OF。

在单片机的ALU中既不会集成图3.2.14的数据比较器，也不会集成图3.2.19的十进制运算器，那样会使ALU很臃肿，硬件开销太大。要比较两个数A和B的大小通过编程实现，只需进行一次A－B的运算，然后根据运算结果标志位即可判定。例如针对无符号数A≤B的条件是：CF+ZF=1；针对有符号数A≤B的条件是：（OFSF）+ZF=1。若针对十进制数（8421BCD）运算，编程者是借用二进制运算器进行运算，并关注标志位AF和结果是否出现伪码，以决定对运算结果的修正。

综上所述，因为ALU中的加法器是最繁忙的部件，所以通过增加硬件的复杂度来提高运算速度，即以牺牲空间换取时间。但是为了使ALU不太复杂臃肿，通常在ALU中不会集成十进制运算器和数据比较器，毕竟十进制运算和数据比较不是很频繁的，通过编程也可以实现，即以牺牲时间换取空间。在数字系统设计中，一般硬件可以软化，软件也可以硬化。要追求速度应从硬件入手，要精简电路降低成本和功耗应从软件入手。总之根据实际情况在软硬件两个方面达到合理的取舍。