1.组合逻辑电路的特点

组合逻辑电路是由与、或、非三种基本逻辑门组合而构成的电路，该电路不含存储元件且无反馈电路，输出状态仅取决于当时的输入状态，与时序信号无关。图3.1.1所示是组合逻辑电路框图，其输出信号是关于全部或部分输入变量的逻辑函数。

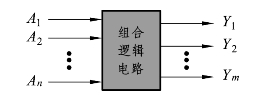
图3.1.1　组合逻辑电路框图

2.组合逻辑电路的分析方法

由给定电路逐级推导逻辑函数式→化简逻辑函数式→根据逻辑函数式列逻辑真值表→根据逻辑真值表确定电路的逻辑功能。

【例3.1.1】 设A，B，C，D为8421BCD码输入信号，试分析图3.1.2中电路的逻辑功能。

解：（1）图3.1.2（a）的逻辑函数为，根据逻辑函数式列出真值表（见表3.1.1，只列出A、B、C、D取值为8421码的状态行）。

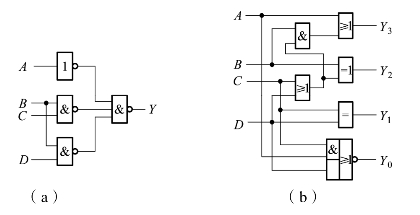
图3.1.2　例3.1.1的电路(www.daowen.com)

表3.1.1　图3.1.2（a）的真值表

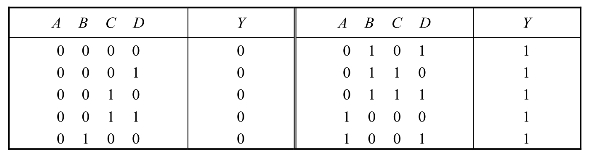
由真值表可知，当A、B、C、D的值小于5时，Y＝0；当A、B、C、D的值大于等于5时，Y＝1。所以该电路的功能是“四舍五入”。

（2）图3.1.2（b）的逻辑函数为

根据逻辑函数式列出真值表（见表3.1.2，只列出ABCD取值为8421码的状态行）。

表3.1.2　图3.1.2（b）的真值表

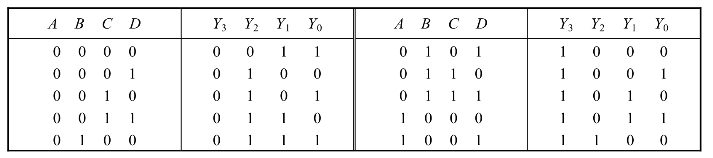
由真值表可知，该电路的功能是将输入的8421BCD码转换为余3码输出。

用74HC00设计举重裁决电路