1.逻辑相邻
如果两个逻辑最小项中仅有一个因子不同,则称这两个最小项逻辑相邻。在卡诺图中,下列情况能直观地反映最小项的逻辑相邻:
(1)相邻两格;
(2)同一行的最左边与最右边两格;
(3)同一列的最上边与最下边两格;
(4)在5、6变量卡诺图中,轴对称位置上的两格。如图1.3.1(c)中的m27和m31;
(5)将5、6变量卡诺图视为由多个4变量卡诺图组成,若在其中的4变量卡诺图中逻辑相邻,那么在5、6变量的卡诺图中也逻辑相邻。如图1.3.1(c)中的m8和m10。
2.用卡诺图化简逻辑函数的方法(1)将逻辑函数表示在卡诺图中。
(2)合并最小项:两个逻辑相邻项合并为一项并消去那个不同的因子;四个逻辑相邻项合并为一项并消去那两个不同的因子;八个逻辑相邻项合并为一项并消去那三个不同的因子……。
(3)合并最小项的原则:①尽可能将矩形圈画大一些,每个圈中有2n个“1”;②每个圈中至少有一个未被圈过的“1”;③孤立项不能化简;④尽可能减少总圈数。
【例1.3.3】用卡诺图将下列逻辑函数化简为最简与或式。

【说明】如果逻辑函数本身是与或式,就不必将其化为标准式,可以直接将逻辑函数写入卡诺图中。例如将Y1中的![]() 视为0×11,将ABC视为111×;将Y3中的AC视为1×1×,将
视为0×11,将ABC视为111×;将Y3中的AC视为1×1×,将![]() 视为××0×。“×”表示取任意值,即需要则视为1,不需要则视为0。在卡诺图中,含一个“×”的与项占2格,含两个“×”的与项占4格,含三个“×”的与项占8格……。合并最小项时,将上述方法反过来操作。例如,如图1.3.2所示,图1.3.2(a)中右下角的圈中有2个“1”,表示为1×10;图1.3.2(b)中右边的圈中有4个“0”,表示为××10。
视为××0×。“×”表示取任意值,即需要则视为1,不需要则视为0。在卡诺图中,含一个“×”的与项占2格,含两个“×”的与项占4格,含三个“×”的与项占8格……。合并最小项时,将上述方法反过来操作。例如,如图1.3.2所示,图1.3.2(a)中右下角的圈中有2个“1”,表示为1×10;图1.3.2(b)中右边的圈中有4个“0”,表示为××10。
解:图1.3.2(a)中含有4个“1”的那个圈是多余的,称为冗余项或蕴藏项,它的每一个“1”都是其他圈已圈过的。除了冗余项,最后得到的都是逻辑素项,或者说最简与或式就是全部逻辑素项之和。
![]()
因为![]() ,作
,作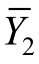 的卡诺图,如图1.3.2(b)所示,用圈“0”法求
的卡诺图,如图1.3.2(b)所示,用圈“0”法求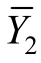 的反函数:
的反函数:


图1.3.2 例1.3.3的Y1、 、Y3卡诺图
、Y3卡诺图
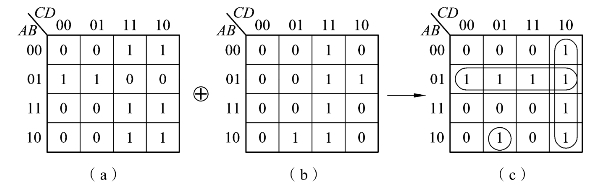
图1.3.3 例1.3.3的Y4卡诺图
将Y4视为两个函数取异或,作这两个函数的卡诺图,并将这两个卡诺图取异或得到Y4的卡诺图,如图1.3.3所示。由图1.3.3(c)可知
![]()
Y5的卡诺图有多种圈法,按图1.3.4(a)和图1.3.4(b)分别得(https://www.daowen.com)
![]()
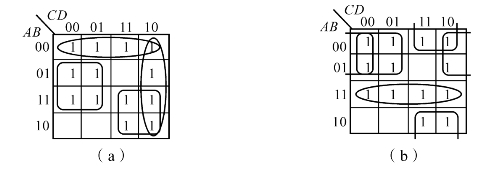
图1.3.4 例1.3.3的Y5卡诺图
【说明】① 两个逻辑函数进行与、或、异或、同或运算,可以用两函数的卡诺图的对应方格进行与、或、异或、同或运算。② 有时利用卡诺图化简得到的函数式不相同,即逻辑函数的最简与或式未必是唯一的,但是得到的逻辑素项的个数以及每个逻辑素项所含的变量数是一致的。
【例1.3.4】用卡诺图将图1.3.1中的逻辑函数Yb和Yc化为最简与或式。

3.具有约束条件的逻辑函数的卡诺图化简
1)逻辑函数中的约束项
在实际电路中根本不可能出现或即使出现也不影响电路的逻辑功能的那些逻辑最小项称为约束项或无关项,记为md。既然md不影响逻辑函数Y,所以∑md应恒为0。通常将∑md=0称为逻辑函数的约束条件。
【例1.3.5】设输入数据为十进制数(8421BCD),求其“四舍五入”标识函数F的标准式。
解:8421BC D对应的十进制数为0~9。当输入数据D3D2D1D0为0~4时F=0,当输入数据D3D2D1D0为5~9时F=1,所以F=∑mi(i=5,6,7,8,9)。
另外8421BCD的伪码应为无关项,所以∑md(d=10,11,12,13,14,15)=0。带约束条件的逻辑函数标准式可表示为:
F(D3,D2,D1,D0)=∑mi(i=5,6,7,8,9)+∑md(d=10,11,12,13,14,15)
2)用卡诺图化简具有约束条件的逻辑函数
(1)将逻辑函数中的逻辑最小项用“1”表示在卡诺图中,将约束条件中的约束项用“×”表示在卡诺图中。若某方格出现“1”和“×”重合,该方格应填“1”。
(2)合并最小项和约束项:尽可能将矩形圈画大一些,每个圈中可以有任意多个“×”,但至少有一个未被圈过的“1”。
【例1.3.6】用卡诺图将下列具有约束条件的逻辑函数化简为最简与或式。
Y1=![]() ,约束条件AB+AC=0。
,约束条件AB+AC=0。
Y2(A,B,C,D)=∑mi(i=2,4,6,7,12,15)+∑md(d=0,1,3,8,9,11)
Y3(D3,D2,D1,D0)=∑mi(i=5,6,7,8,9)+∑md(d=10,11,12,13,14,15)
解:作Y1,Y2和Y3的卡诺图,如图1.3.5所示。

图1.3.5 例1.3.6的Y1、Y2和Y3卡诺图
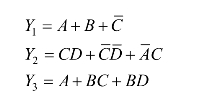
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






