卡诺图是美国工程师Karnaugh于20世纪50年代提出的，它可以将任何逻辑函数方便地化为最简与或式。n个变量的卡诺图由2n个方格组成，每个方格对应一个逻辑最小项。图1.3.1是3变量、4变量和5变量的卡诺图。2变量的逻辑函数化简很简单，不必使用卡诺图。6变量卡诺图可以参考5变量卡诺图画出，在此省略。超过6个变量的逻辑函数化简不能直接使用卡诺图，可以将该逻辑函数分解为多个变量数较少的逻辑函数后，再使用卡诺图化简。

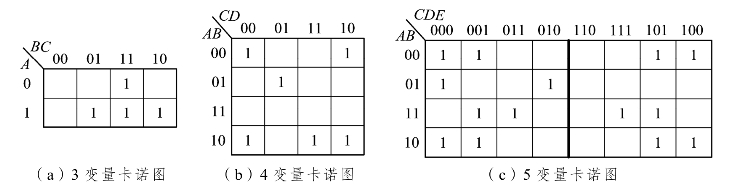
如图1.3.1所示，3变量卡诺图的纵坐标^[1]取值依次为0和1，横坐标*取值依次为00，01，11，10；4变量卡诺图的坐标值可以根据三变量卡诺图推得；5变量卡诺图可以看作两个四变量卡诺图对称排列，左边4变量卡诺图的横坐标依次为00，01，11，10，右边4变量卡诺图的横坐标依次为10，11，01，00。然后在左4变量卡诺图各坐标值的前面添0，在右4变量卡诺图各坐标值的前面添1。这就不必死记硬背5、6变量卡诺图的坐标值了。

(www.daowen.com)

图1.3.1　3、4、5变量卡诺图

用卡诺图表示某逻辑函数的方法是：首先将逻辑函数化为标准式，然后将其逻辑最小项以“1”的形式填入对应方格中，习惯上纵坐标在前横坐标排后构成逻辑最小项的对应值。在图1.3.1中，各卡诺图表示的逻辑函数分别是