由逻辑真值表写原（反）函数表达式的方法：选取函数值为1（0）的状态行相或，每行的状态决定变量组成一个与项，状态行中取值为1的记为原变量，取值为0的记为反变量。

【例1.2.2】两个二进制数A＝AnAn－1…Ai…A0，B＝BnBn－1…Bi…B0相加，其中第i位的运算是Ai加Bi再加来自低位的进位Ci－1，产生本位的和Si以及向高位的进位Ci，能实现这种运算的电路叫作一位全加器，试推导其逻辑函数式并画出电路图。

解：① 根据二进制加法运算法则得逻辑真值表，如表1.2.4所示。

表1.2.4　一位全加器真值表

② 由逻辑真值表得逻辑函数式并化简(www.daowen.com)

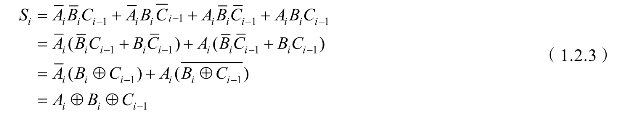
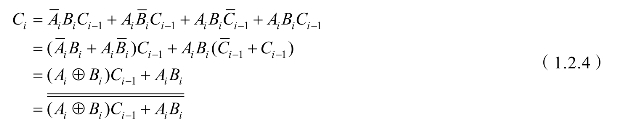
③ 根据式（1.2.3）和式（1.2.4）得电路图，如图1.2.2所示。

【说明】如何确定逻辑变量之间是“与”关系还是“或”关系呢？真值表中的一个状态行是某时刻若干个变量的取值，同时性或者说相容性决定“与”关系；真值表中不同的状态行是不同时刻若干个变量的取值，先后性或者说相斥性决定“或”关系。例如夫妻A、B乘地铁回家要过两种门，夫妻通过同一匝道进地铁这一事件是由A、B相或决定的；夫妻进家门这一事件是由A、B相与决定的。

图1.2.2　一位全加器电路