由于使用要求的需要，工业上实际使用的金属中大多是三元或多元合金，仅仅铁碳相图已经不能满足使用。学习三元、多元相图，对分析材料的成分、组织与温度的变化关系，预测材料的组织与性能的都十分必要，可为制订热处理工艺提供帮助。

1.三元相图的表示方法

由于多元合金相图的复杂性，在测定和分析等方面受到限制，因此用得较多的是三元合金相图。

三元相图与二元相图比较，组元数增加了一个，即成分变量是两个，故表示成分的坐标轴应为两个，采用一个平面等边三角形来表示。相图三角形的三个顶点代表纯组元A、B、C的，三个边长各定为0～100%的合金成分，分别表示二元系即A-C、C-B、B-A系。一般在三角形中画出平行于各边坐标的网格，见图1-26。图中的X点的组元含量确定方法：经过X点平行于BC的直线与CA、AB边的交点，分别是20%、80%，即C-A系合金中，A组元的质量分数是20%，A-B系合金中，B组元的质量分数是80%，同样方法得到与BC边相交的点40%，即B-C系合金中，C组元的质量分数是40%。

平行于三角形某一条边的直线表示：凡成分位于该线上的合金，它们所含由这个边对应顶点所代表的组元含量是一定的。例如，如图1-26所示，线段de线上的所有合金，C组元的质量分数都是相等，即20%。

通过三角形顶点的任一直线表示：凡成分位于该直线上的合金，它们所含由另两个顶点所代表的两组元的含量之比是一定的。例如，如图1-26所示，位于CP线上的任意合金的A、B组元的含量比值一定，即w（A）/w（B）=BP/AP。

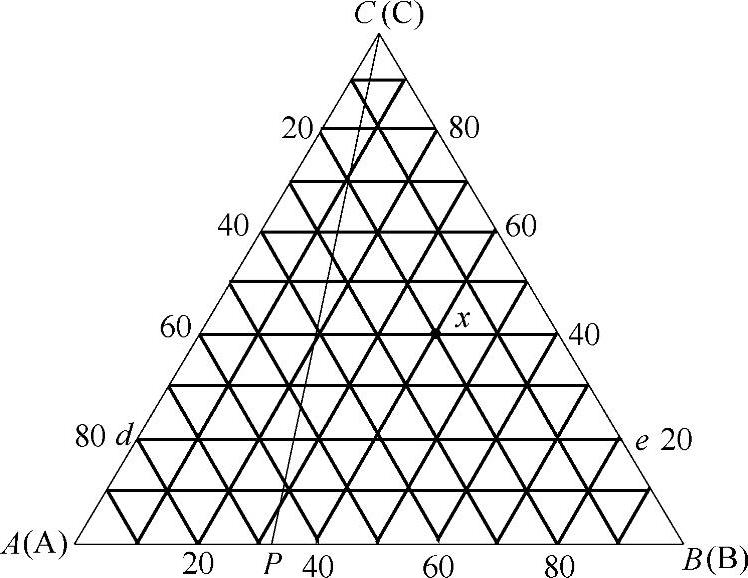
图1-26 三元相图

在三元相图中，合金的相对含量使用重心法则计算。三元相图中空间三相区是以三条单变量线作为棱边的空间三棱柱体，因此三相区的水平截面一定是三角形，三角形的三个顶点代表在此温度下三个平衡相的成分，三个组成相两个之间相平衡，三角形的边就是两个平衡相的共轭线，这个三角形反映了某温度下三个平衡相成分之间的对应关系，叫做共轭三角形。如图1-27所示，ijk三角形就是共轭三角形，合金成分O在某一温度下，由α、β、γ三相组成，成分分别是i、j、k。合金成分O一定位于ijk三角形的质量重心，合金中α、β、γ三相的质量分数为

w（α）=（Ot/it）×100% （1-7）

w（β）=（Os/jg）×100% （1-8）(www.daowen.com)

w（γ）=（Or/kr）×100% （1-9）

上面三式就是三元系合金的重心法则。

图1-27 重心法则

2.相区接触法则

三元相图相区接触法则与二元相图相同，即相邻相区的相数相差1，无论在何种形式的相图中都遵循这个法则。相图截面上的点都应该与4根线相连。

3.三元系合金四相平衡转变类型

在三元系合金的垂直截面图上，一般可能出现的四相平衡转变见图1-28。

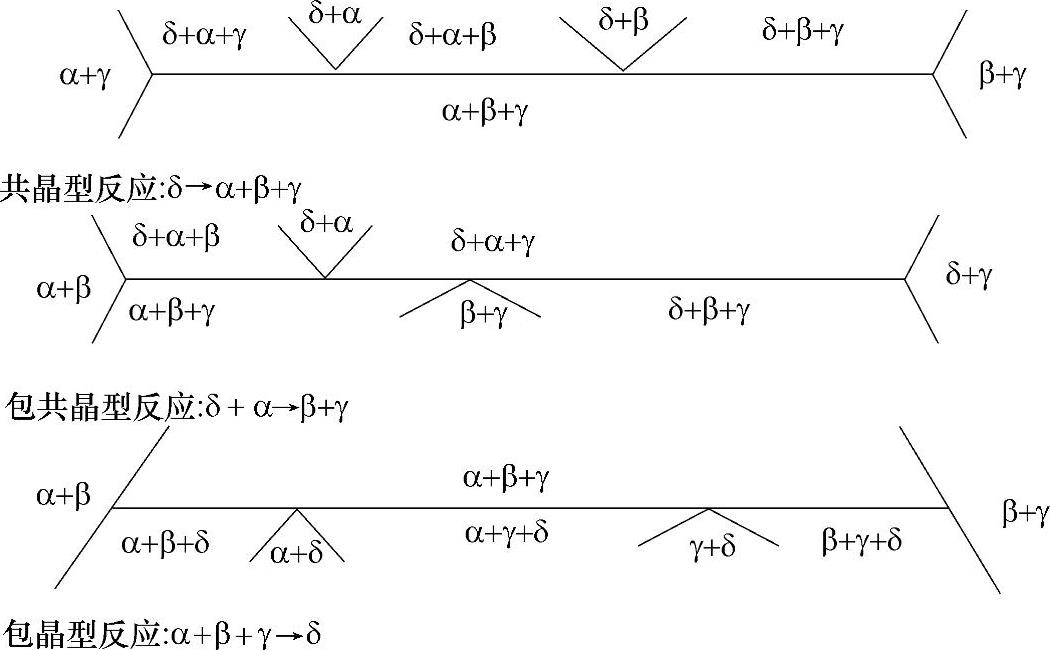
图1-28 三元系合金四相平衡转变类型