4.5.2.1 电压矢量对有功无功的影响

由上分析，非零矢量的作用是让转子磁链沿着它的方向移动运行，零矢量的作用使转子磁链停留在原地，等待下一个非零矢量的到来。综合式（4-38）和式（4-39）可以得到在以转子速度为同步速的两相旋转坐标系下的表达式：

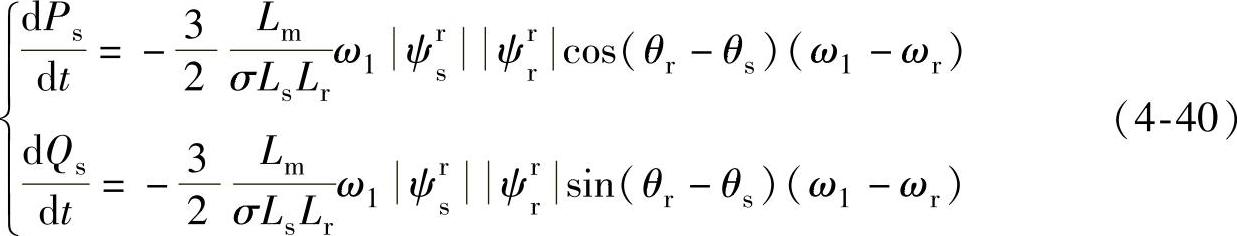
上式显示了非零电压矢量对有功功率和无功功率的作用效果在电机运行于超同步速和亚同步速时是完全不同的。在超同步速时（ω₁-ω_r）＜0，零电压矢量减少有功输入和无功输出，在亚同步速时的作用效果相反。

由以上分析可知，电压矢量能使转子磁链向靠近给定电压矢量的方向移动。只要已知转子磁链位置，就可以求出每个电压矢量对转子磁链的调节作用。进一步可以得到这些电压矢量对变量的调节作用，这样有功功率和无功功率的控制就转化为对这八个电压矢量的调节。

其中ψ^r_r可以由公式（4-39）来计算，但是当转速较低时转子电压较小，这样转子电阻造成的压降不可忽略，正是由于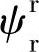求解的精度问题，可以用较为恒定的定子磁链进行替代，可按下式来进行替换：

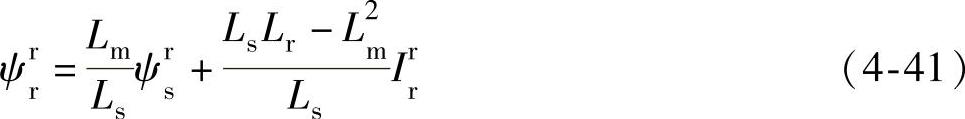
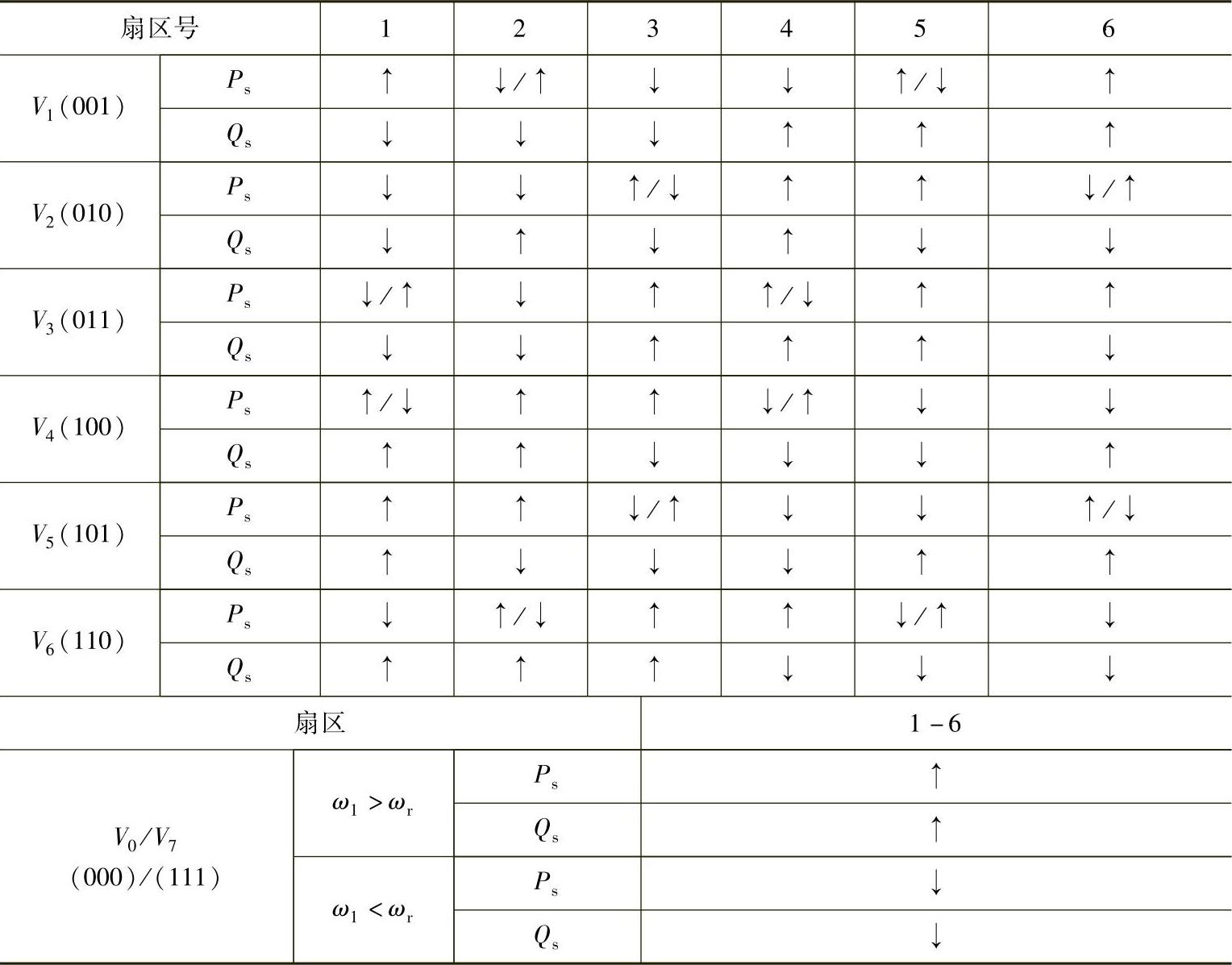
依照定子磁链位置，八个开关电压矢量对有功功率和无功功率的作用效果列为表4-2：

表4-2 开关电压矢量对功率作用效果表（↑增加；↓降低）

4.5.2.2 直接有功无功控制

通过合适的选择开关电压矢量，就可以对有功功率和无功功率进行高效的动态控制，这就是直接功率控制的基本原理。选择方法如下：首先将有功功率和无功功率与其给定值进行比较，由两电平的滞环比较器根据误差来产生有功功率、无功功率状态量S_p、S_q，其中S_p、S_q是通过一个容差为100的滞环比较器获得，滞环比较器原理如图4-18所示。当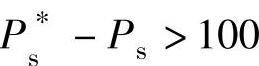时，则S_p=1，表示当前的输出有功功率实际值偏小，要达到有功功率的给定值，必须选择一个电压矢量使磁链增加。以扇区2为例：可以选择u₄、u₅使有功功率增加，其他扇区可以类推。

当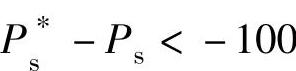时，则S_p=-1，表示当前的输出有功功率实际值偏大，要达到有功功率的给定值，必须选择一个电压矢量使有功功率减小。以扇区2为例：就可以选择u₂、u₃使磁链增加，其他扇区类推。

当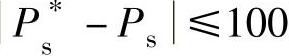时，则S_p保持不变。无功功率控制与此相似，不再赘述。

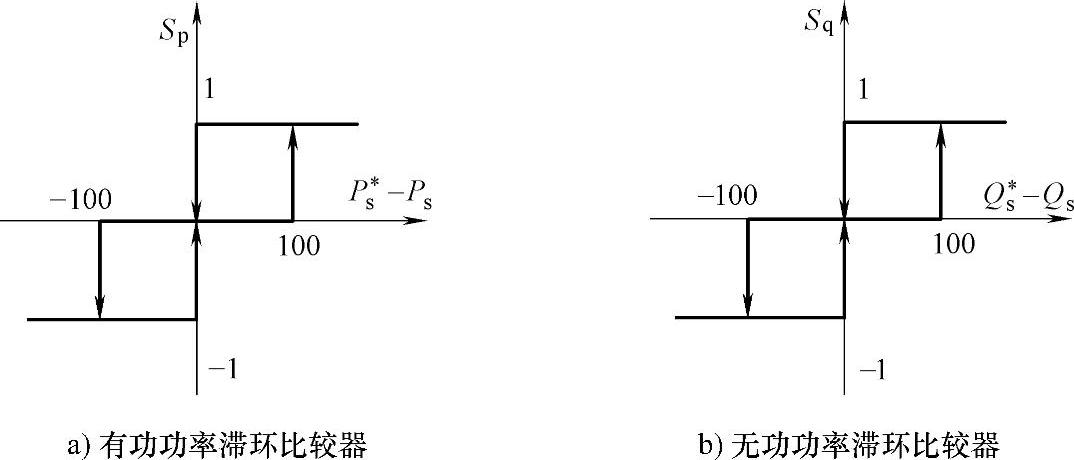
图4-18 滞环比较器原理

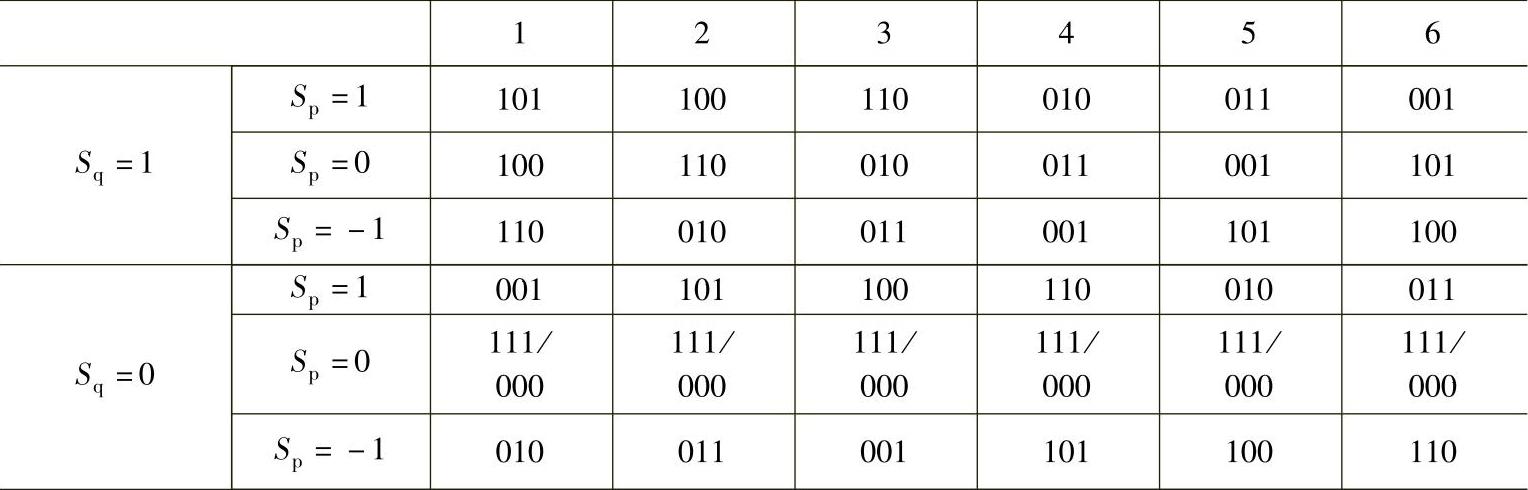
由于最佳开关表的生成不仅考虑非零电压矢量的作用效果，还根据每次开关动作数最小的原则来选择零矢量，使输出无功功率和有功功率能够高效地跟踪给定值。所以，根据有功、无功功率状态量和定子磁链位置，可得表4-3所示的最佳开关表来选择相应的电压矢量。

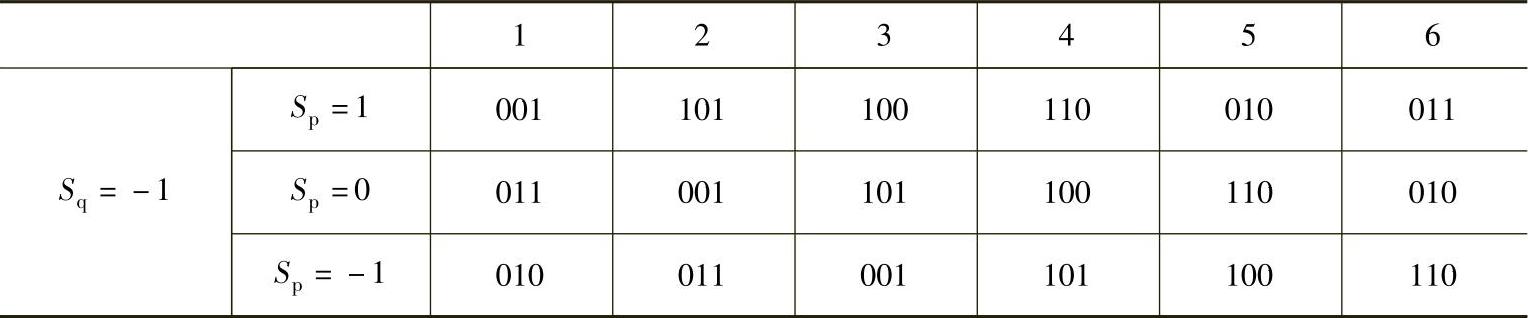
表4-3 直接功率控制最佳开关表

(www.daowen.com)

（续）

4.5.2.3 定子磁链的计算

为了计算旋转坐标系下的定子磁链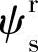，先必须计算在静止坐标系下的定子磁链ψ^s_s的值。在静止坐标系下，定子磁链可以通过下式计算得到：

磁链观测一般采用的模型有三种形式：u-i模型、i-ω模型、u-ω模型。

u-i模型法是用定子电压与定子电流来确定定子磁链的方法，u-i模型定子磁链可以由式（4-43）表示，其结构图如图4-19所示。

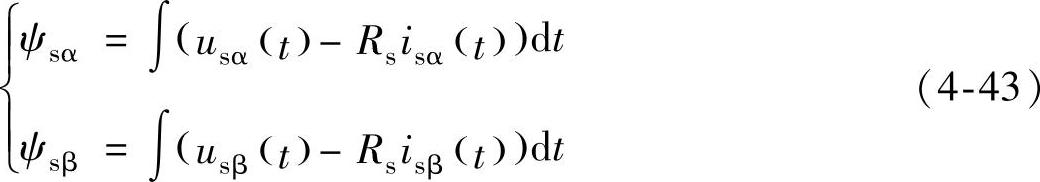
此观测模型只用到一个电机参数，即易于测量的定子电阻R_s，式中的定子电压u_s（t）和定子电流i_s（t）同样也是易于确定的物理量，它们能以足够高的精度被检测出来。该模型结构简单，在理论上很精确，但当转速很低时，电阻R_s上的压降占电压的绝大部分，因此e（t）=u_s（t）-R_si_s（t）接近零。这样测量误差将把e（t）掩盖掉，也就造成了观测不准确。由于本书的重点不是对基于直接功率控制的双馈感应电机低速性能进行研究，且为了简化结构和易于实现，所以磁链观测模块在仿真时选用u-i模型。

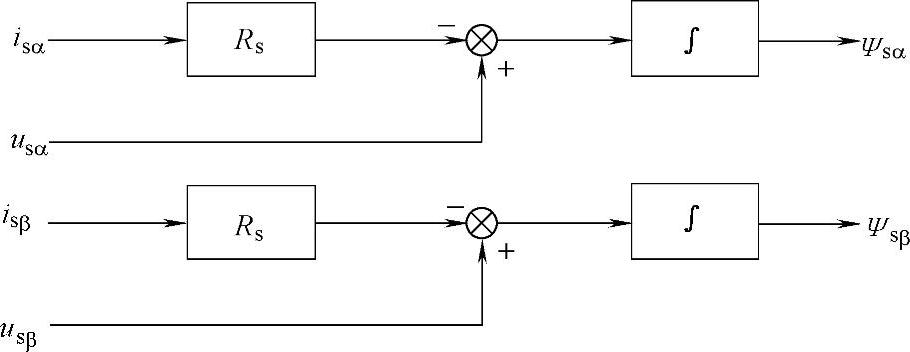
图4-19 定子磁链的u-i模型结构

此外，i-ω模型受转子电阻、漏电感、主电感变化的影响，尤其是转子时间常数，它们也随转速的变化而变化，高速时此模型的观测结果不如电压模型准确；u-ω模型作为一种实用和简单的磁链观测器，在本书第6章有具体应用，可检测出电压和磁链的相位关系。

因为定子电压谐波含量少和频率固定，所以式（4-34）能够得到较精确的定子磁链。旋转坐标下的定子磁链ψ^r_s可以通过式（4-32）计算得到。

4.5.2.4 直接功率控制原理图

综上所述，得到基于最佳开关表直接功率控制的双馈式风力发电系统原理图，如图4-20所示。其中，每个采样周期里由有功功率和无功功率滞环控制器输出有功和无功功率的控制量S_p、S_q，再结合定子磁链在扇区的具体位置，根据最佳开关表便可以输出最佳的电压矢量。

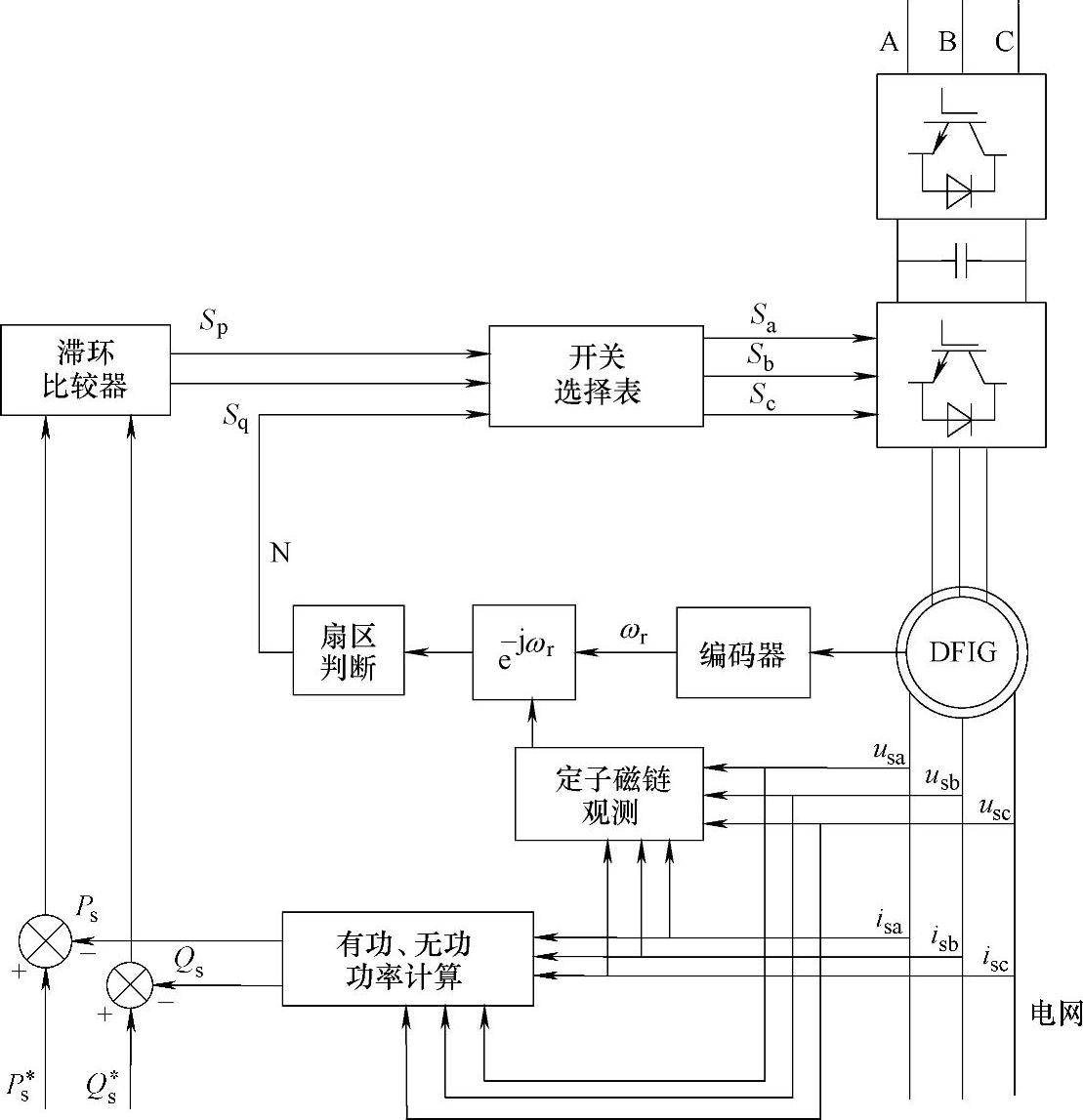
图4-20 直接功率控制原理图