胡春宏（1995）在水槽试验中用高速摄影技术获得大量泥沙运动轨迹的资料，据此分析了颗粒各种运动形式的力学和统计特性。试验水槽长16m、宽0.5m，水深5～12cm，坡降0.1%～1.4%，槽底为光滑和粗糙两种情况。采用了5种不同比重（γS=1.043～2.65）的沙样，粒径D=1.23～7.6mm。图5-1为各种粒径和比重的泥沙颗粒的各种运动形式所占的百分比与Shields数Θ[=γhJ/（γS—γ）D]的关系，图5-2则为跃移质占整个推移质的百分比与Θ的关系。结果表明，当Θ=0.2时，跃移已占整个泥沙运动的60%以上，即跃移质是推移质运动的主要形式，因而有必要进行深入研究。

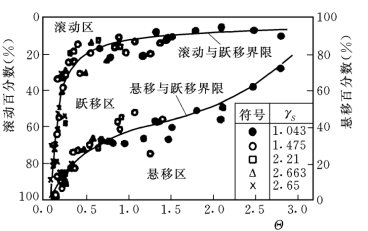
图5-1　颗粒各种运动形式所占百分比与Θ的关系

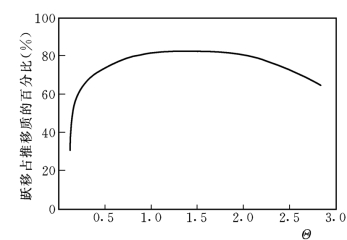
图5-2　跃移占整个推移质的百分比与Θ的关系

颗粒跃移的轨迹和相关参数的定义见图5-3，其中Hb为跃高，L为跃长，L1为跃高点的长度，Ub为平均纵向跃移速度，为跃移速度，Ub0和Vb0及Ube和Vbe为起跃点及降落点的相应分速。

图5-4为跃移颗粒分速的沿程变化过程，颗粒在起跃阶段的变化比较剧烈，起始的垂向速度较大，继之沿程减小，到跃高点时为0，其后则方向向下；纵向速度沿程不断加大，在跃高点以后趋于常数值。

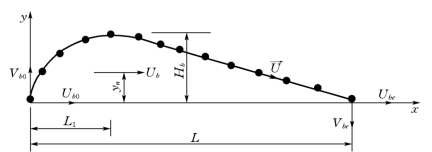
图5-3　颗粒跃移参数的定义

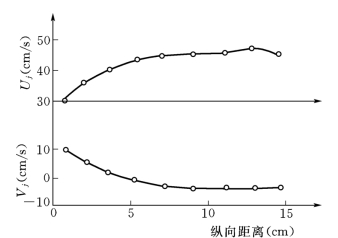
图5-4　跃移颗粒速度的沿程变化过程

平均纵向跃移速度Ub与床面的粗糙程度有关，见图5-5，图中的资料为5种不同比重沙样（与图5-1的沙样相同）的结果，从图中难以分辨比重的明显影响。

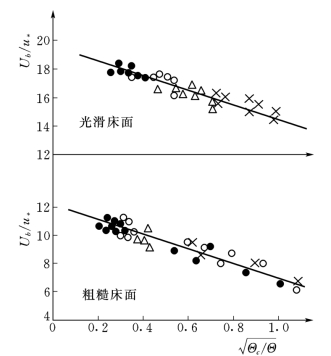
图5-5　不同床面条件下跃移速度的变化规律

图中的回归线可表示为(www.daowen.com)

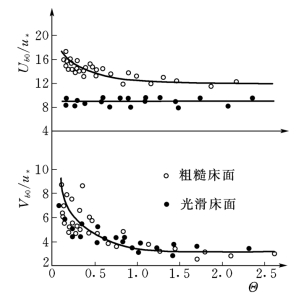
图5-6　起跃速度与水流强度的关系

颗粒跃移的初始速度与Θ的关系见图5-6，其纵向分速与床面粗糙条件有关

跃移颗粒降落点的速度亦存在类似的结果，对纵向分速

知道两个方向的分速以后，可以分别计算跃移颗粒的起跃角和降落角。

跃移颗粒的跃高和跃长与泥沙颗粒的比重和床面的粗糙情况有关，可分别表示为

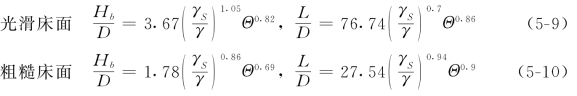
对大量实测资料的统计分析表明，相对跃高和跃长的概率密度分布与床面粗糙情况无关，均服从Г分布

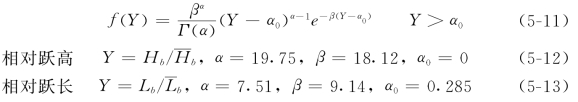
各种实测资料的结果表明，平均跃长与跃高点长之比为接近3的常数，具有很好的规律性。在得出跃长和跃高的数据后，可以计算其比值。分析结果表明，随水流强度而增加，且光滑床面时比粗糙床面时为大。