在介绍Shields的起动拖曳力曲线时提到，当Re*=10时，起动拖曳力最小，在曲线左端随着粒径的变细，起动拖曳力反而增加，这主要是粘结力在起作用。

张瑞瑾（1989）认为细颗粒之间的粘结力主要是由于存在于颗粒之间的吸着水和薄膜水不传递静水压力所引起的。粘结力主要与沙粒之间的空隙、沙粒在水平面上的投影及沙粒所受垂直下压力有关，经过推导，得出了起动流速的表达式

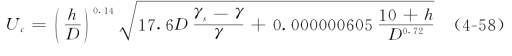
窦国仁（1960）通过石英丝的试验，明确了颗粒的受力情况，证实了薄膜水的一些物理性质，并在此基础上推导出了一个适用于各种颗粒的起动流速公式

H a=10m，为以水柱高表示的大气压力，δ0=3.0×10—8 cm为水分子厚度。

窦国仁（1999）还从式（4-3）出发，采用时均流速分布公式求出垂线平均流速Uc=2.5u*ln（11h/ks）及时均底流速U0c=5.54u*（y=ks/2），则Uc=0.451ln（11h/ks）U0c，代入式（4-3）得出

式中：ks为床面粗糙高度。

各公式的对比见图4-19，当水深为15cm、D＜0.1mm时的起动流速基本一致，D＞0.2mm后，各公式的差异较大。(www.daowen.com)

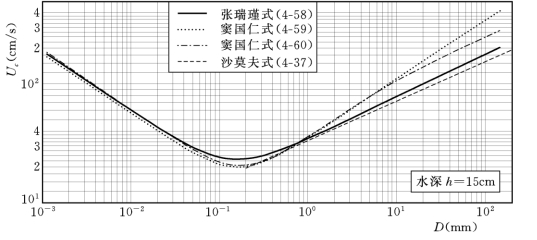
图4-19　各起动流速公式的对比

水深为15m时各公式的对比见图4-20，当D＜0.1mm时，式（4-58）和式（4-59）的结果一致，但式（4-59）与式（4-60）有很大的差异。分析结果表明，D＜0.1mm的起动流速可用式（4-58）或式（4-59）计算，当D＞0.2mm时，各公式的差异较大。

图4-20　各起动流速公式的对比

Roberts（1998）试验研究了细泥沙颗粒的粒径和密度对临界起动应力的影响，结果见图4-21。从图中可以看出，当粒径D＞0.1mm时，淤积物的密度对临界起动应力的影响不大；当D＜0.1mm后，随着淤积物密度的增加，同粒径的泥沙颗粒的临界起动应力明显加大。作者认为，细颗粒泥沙的临界起动应力随密度而变化主要是受粘结力的影响，在粘结力的影响机理不是很清楚的情况下，还难以提出相应的无量纲化参数，所以图4-21采用了临界起动应力与粒径的直接关系而不是Shields曲线的参数。

图4-21　临界起动应力与粒径和密度的关系

Krone（1999）进一步研究了Roberts（1998）和Zreik（1998）的试验资料后认为，影响粘性泥沙颗粒起动的主要因素是其在床面形成的结构。随着覆盖层的增加，絮凝结构将逐渐崩解而更加密实，从而更难于起动。

万兆惠（1990）研究了水压力对泥沙起动的影响，在专门设计的设备中，最大水压力可到10m水柱。对于散粒体泥沙（试验沙D=0.065mm），起动流速与水压力无关。对细颗粒泥沙（D=0.004mm），起动流速随水压力的增加而明显加大，试验结果介于窦国仁公式和张瑞瑾公式之间。