（一）无粘性颗粒含沙水流的粘滞系数

A.Einstein假定固体颗粒为均匀球，浓度很低，颗粒与颗粒之间互不接触，于1905年发表了从理论上推导得出的极稀含沙水体粘滞系数公式

其中μ0为清水粘滞系数，Sv为体积含沙量。式（1-55）只适用固体颗粒浓度极低的情况。沿这一思路所进行的其他研究，其应用范围大部分限于均匀球形颗粒的悬液，而且浓度不能过高。表1-19所示是这类结果中的有代表性的一部分。

这类无粘性细颗粒的含沙水流，一般都属于牛顿流体，没有屈服应力。费祥俊（1994）提出了如下经验公式表达含沙水流的相对粘滞系数

其中μ0、μr分别为清水粘滞系数和含沙水流的相对粘滞系数；Sv为泥沙体积比浓度，Svm为极限体积比浓度，也就是粘性达到无穷大时的含沙量。

表1-19　牛顿体悬液相对粘滞系数公式（转引自费祥俊1994）

（二）含有粘性细颗粒的悬液粘度

当悬液中含有足够多的粘性细颗粒时，细颗粒的特殊物理化学性质将引起相同体积比浓度下粘滞系数的增加，并使含沙水流出现屈服应力，使悬液转化为非牛顿流体。对于这种情况，尚无理论上的推导来确定其粘滞系数和屈服应力，但可以从试验结果出发建立经验关系式。表1-20列出了有代表性的几家成果，有关τB更详细的结果可参见费祥俊的研究（费祥俊，1994，表2-3）。(www.daowen.com)

表1-20　含有粘性细颗粒的悬液粘度经验关系式

注　τB的单位为N/m2。表中的μr实际是宾汉体的刚度系数。

粘性细颗粒的悬液粘度研究目前所存在的主要问题，是公式中不能反映出泥沙颗粒级配的影响，特别是极其重要的细颗粒含量的影响。费祥俊对粒经组成的影响进行了分析，推导得到了如下宾汉体相对刚度系数表达式

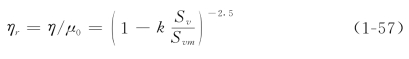
其中k是考虑封闭水影响对有效浓度系数的修正，由实验结果可得出

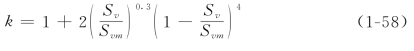
含沙水流从牛顿体过渡到宾汉体的临界浓度与D＜0.01mm的细颗粒含量有很大关系，如图1-22所示（费祥俊1994，43页）。此外，粒径的矿物成分，水中离子的种类和含量对含沙水流的粘性都有很大的影响。

图1-22　牛顿体过渡到宾汉体的临界浓度