4.3.2.1　深水测试井筒温度分布计算

井筒压力剖面计算极大地依赖于井筒温度剖面的预测，常规的方法是假设井筒温度剖面线性化，井筒流体温度与时间无关，这种处理方式对处于稳定生产状态的油气井压力计算是合适的，但是在油气井不稳定测试过程中流量、压力、温度可能都处于不稳态过程，在此情况下沿用常规方法估计井筒温度误差较大，导致压力计算偏差。本研究针对试采阶段的长期稳定生产过程，采用解析方法建立井筒稳态传热模型，预测非线性井温剖面；针对试油测试的短期过程，建立井筒非稳态传热模型，预测不同测试制度和时间下的井温剖面。

当气体从井底沿井筒向上流动时，由于气体和井筒周围地层之间存在温差，因此必然通过导热、对流和辐射三种传热方式向周围地层传热。为将三维热扩散问题简化为一维径向热流，假设如下：

①生产过程中动能忽略不计。

②地温按线性分布，且井底流体温度等于地层温度。

③井筒及地层中的热损失是径向的，不考虑沿井深方向的传热，且井筒中任意截面上各点的温度均相等。

井筒流体向外传递热量时，由于热对流和热辐射占总传热的比例很小，因此可以忽略不计。取长为d h的微元为控制体，在海床以下部分可以得出控制体与井筒的流体瞬时传热速度

式中　rt——油管内径（m）；

Uo——井筒总传热系数［J／（m2·s·℃）］；

Ts——井筒内流体温度（℃）；

Th——水泥环与地层交界处的温度，为时间的函数（℃）。

钢材具有很高的热传导率，因此油管和套管的热阻可忽略不计，则Uo计算式为

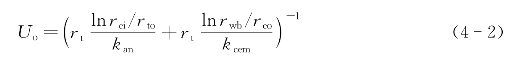
式中　rci——套管内径（m）；

rto——油管外径（m）；

kan——环空导热系数［J／（m·s·℃）］；

rwb——裸眼井径（m）；

rco——套管外径（m）；

kcem——水泥环导热系数［J／（m·s·℃）］。

井筒周围地层中的热传导是一个不稳定传热过程，采用Ramey近似公式计算地层瞬时传热速度：

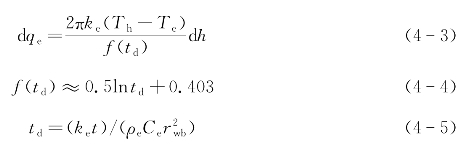
式中　ke——地层导热系数［J／（m·s·℃）］；

Te——地层温度（℃）；

td——无因次时间；

t——热扩散时间（s）；

ρe——地层岩石密度（kg／m3）；

Ce——地层岩石比热［J／（kg·℃）］。

由式（4-1）、式（4-3）可以得到井筒流体在海床以下部分的总瞬时传热速度计算式

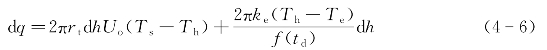
根据能量和温度的关系，可以得到控制体温度变化的计算式

式中　Cm——井筒流体的定压比热［J／（kg·℃）］；

w——流体质量流量（kg／s）。

在海床以上部分，考虑到深海天然气井有很长一部分井段在隔水套管中，则温度计算公式改写为

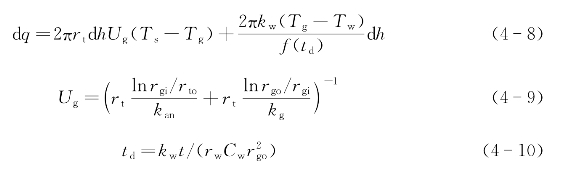
式中　Ug——隔水管总传热系数［J／（m2·s·℃）］；

Tg——隔水管与海水交界处的温度（℃）；

kw——海水导热系数［J／（m·s·℃）］；

Tw——海水温度（℃）；

rgi——隔水管内径（m）；

rgo——隔水管外径（m）；

kg——隔水管导热系数［J／（m·s·℃）］；

Cw——海水比热［J／（kg·℃）］。

4.3.2.2　深水测试井筒压力分布计算

计算气井井底压力的方法很多，其中Cullender和Smith提出的模型至今仍为气藏工程中井筒压力计算的首选方法。气井产出物从井底沿油管流到井口的总能量消耗中，动能损耗甚小，可以忽略不计。因此，气体稳定流动能量方程式可简化为(www.daowen.com)

式中　ρ——气体密度（kg／m3）；

vg——气体流速（m／s）；

f——Moody摩阻系数。

式（4-11）是在任何状态（p，T）下都成立的能量守恒微分方程式，由式（4-11）可以推导出Cullender和Smith方法用于干气井井筒压力计算的模型，即

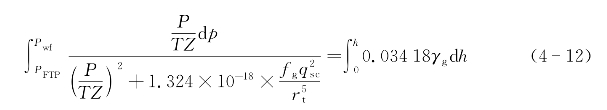
式中　Pwf——井底流压（MPa）；

PFTP——井口流动压力（MPa）；

T——任意井深处井筒内流体温度（℃）；

Z——气体偏差系数；

p——任意井深处井筒内流体压力（MPa）；

fg——气体摩阻系数；

qsc——产气量（m3／d）；

γg——气体相对密度；

h——井深（m）。

由于天然气中可能有冷凝水和凝析油，会直接影响该方法的计算精度。因此对Cullender和Smith方法进行含液修正，以便更准确地计算含液气井井筒压力分布：

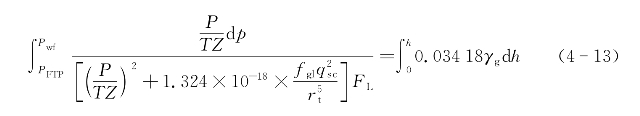
式中　fgl——含水气体摩阻系数；

FL——气体含液校正系数。

4.3.2.3　深水测试过程中水合物生成预测与预防

深海海底泥面低温环境（南海海底泥线附近的温度可能小于3℃）及井下关井后压力迅速减小将是导致水合物生成的主要原因。水合物的形成不仅会造成测试失败而且会大大增加井控风险，甚至带来灾难性事故。抑制水合物生成是深水天然气测试所面临的一个重要问题。

不同油嘴直径和下深位置井下节流后的地层加热效果不同，节流设计须确定控制流量及节流后温度压力下降不会产生水合物，其本质是利用井筒温度剖面和压力剖面，预测水合物的生成条件：如果气体压力低于水合物形成压力、气体温度高于水合物形成温度，则可保障气井正常生产；否则井下油嘴的设计参数（直径、深度）不合理。一般采用热力学方法进行统计。

巴尔列尔和斯丘阿尔特根据严格的统计热力学原理，推导出了预测天然气水合物生产条件的统计热力学算法，其方程的一般形式为

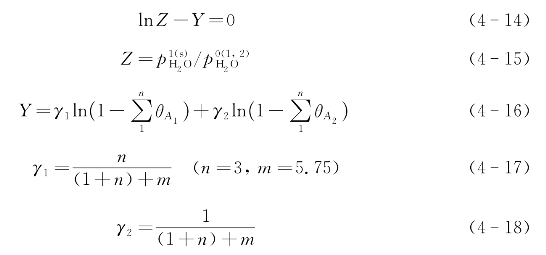
对指定结构的水合物，ln Z是温度和压力的函数。当p≤5MPa时，压力对ln Z的影响非常小，关系式可用两个三项方程（误差约为3.5%）来表示：

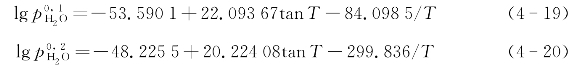
对于不含H2S的天然气，lg Z可用下式求解：

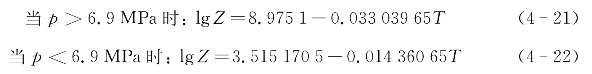
而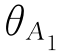和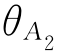分别为气体A在水合物大、小空腔的填充程度，可表示为

式中　i——水合物大、小两种空腔；

j——天然气组成；

Cij——i孔穴j组分的兰格缪尔系数，取

水合物防治方法主要是通过工艺措施，将地层流体在整个测试流程中的温度、压力控制在预测的水合物形成包络线以外。要选用高效的水合物抑制剂（甲醇、乙二醇等）。根据预测计算，实时调整作业过程中水合物抑制剂的注入量大小，选择合适的化学注入泵。

4.3.2.4　实例分析

以中国南海某深水评价井为例。该井水深为1 345 m，完钻垂深为3 887 m，产层顶深为3 142 m，产层厚36 m，孔隙度为24%～28%，渗透率为300×10-3～3 000×10-3μm2，海床温度为3℃，地层压力为32.36MPa，地层温度为90.3℃，地温梯度为0.052 6℃／m，气体密度为0.70g／cm3，气体含水为0.245×10-4 m3／m3，并含有少量凝析油，裸眼完井、筛管防砂、采用11.43 cm油管生产。根据所建立的数学模型，应用以上基础数据，分别计算了不同井口压力、不同产气量条件下的井筒温度分布曲线。

由图4-4和图4-5中的计算结果可以看出，由于深水海床附近温度较低，在靠近海底部分的井筒温度下降明显。井口压力为6.8MPa生产时井筒温度下降幅度较20.5MPa时下降明显，这是因为流体丢失的热量正好是井筒和地层中传播的热量，流体从地层携带出的热量随产气量和压力的降低而减少，因此井筒温度下降幅度随产气量降低而增加。

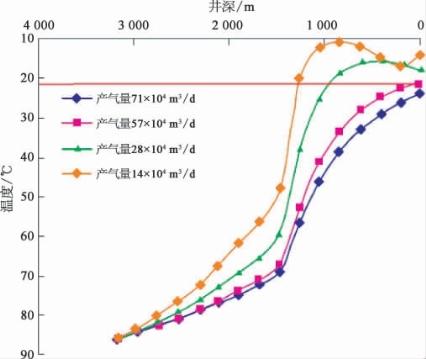
图4-4　井口压力为20.5MPa时井温分布曲线

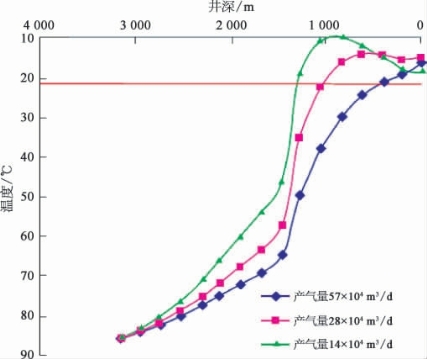
图4-5　井口压力为6.8MPa时井温分布曲线

该井天然气含有少量CO2和微量H2S，参考CH4的临界温度线（图4-4、图4-5中的红线）为井筒天然气水合物生成线，表明在低产气量、低井口压力状态生产测试时，在靠近海床低温地层的井筒及以上部分有大范围生成天然气水合物堵塞井筒的可能。

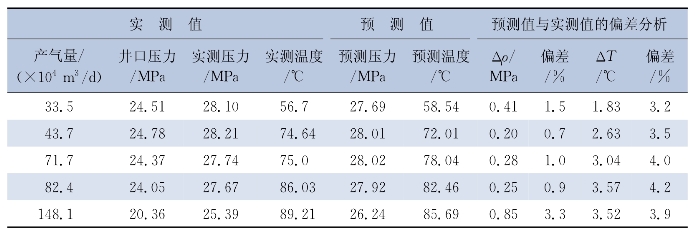
试油测试过程中，在海床位置安装了数据直读系统，来采集油管内壁温度和压力。通过对比可以看出（表4-5），由建立的井筒压力、温度分布预测模型计算得出的压力、温度，与实际值相差均小于4.2%，满足现场要求，可用于实际生产测试。

表4-5　不同产量和井口压力情况下海床温度、压力实测值与预测值