隔水管侧向振动微分方程为四阶偏微分方程：

或

当纯波浪作用时，依据Morison方程计算作用于隔水管的水动力载荷为

式中，最右边第一项为正比于水质点相对速度平方的拖曳力，第二项为正比于水质点加速度的惯性力，第三项为正比于水质点加速度的由于附加质量引起的惯性力。

一种计算理论认为，当波、流同时作用于隔水管时，Morison方程需要进行第一次修正：

由于海流是稳态的，它只对结构产生拖曳力，而不会对惯性力产生影响。但计算拖曳力的水质点速度不是简单将两者相加，而是要计算波浪与海流各自引起的水质点速度的矢量和。

对隔水管进行动态分析时，由于隔水管的运动，需要对Morison方程进行再一次修正，得到

或

上几式中　y——隔水管偏离井口垂直位置的位移；

z——沿着隔水管的垂直距离（起点在泥线）；

t——时间；

E——隔水管的杨氏模量；

I——隔水管的截面惯性矩；

T——隔水管的有效轴向张力；

M——隔水管单位长度质量；

F——作用于隔水管单位长度的流体载荷；

ρ——海水密度；

D——隔水管拖曳力直径；

CM——圆柱体在振荡流中的惯性力系数；

上几式中　y——隔水管偏离井口垂直位置的位移；

z——沿着隔水管的垂直距离（起点在泥线）；

t——时间；

E——隔水管的杨氏模量；

I——隔水管的截面惯性矩；

T——隔水管的有效轴向张力；

M——隔水管单位长度质量；

F——作用于隔水管单位长度的流体载荷；

ρ——海水密度；

D——隔水管拖曳力直径；(www.daowen.com)

CM——圆柱体在振荡流中的惯性力系数；

——波浪水质点加速度；

uc——稳态流速。

采用规则波浪时，规则波水质点速度为uw（z，t）=u0eiωt，u0为水质点速度幅值。假设隔水管动态响应为y（z，t）=y0（z）eiωt+yc（z），y0为隔水管响应幅值，yc为隔水管平均侧向位移。

代入振动方程（3-95）和二次修正的Morison方程（3-99），得到

——波浪水质点加速度；

uc——稳态流速。

采用规则波浪时，规则波水质点速度为uw（z，t）=u0eiωt，u0为水质点速度幅值。假设隔水管动态响应为y（z，t）=y0（z）eiωt+yc（z），y0为隔水管响应幅值，yc为隔水管平均侧向位移。

代入振动方程（3-95）和二次修正的Morison方程（3-99），得到

将上式最后一项进行线性化处理，可得

将上式最后一项进行线性化处理，可得

组合上面两个方程并把与时间有关和无关项分列出，得到与时间有关项为

组合上面两个方程并把与时间有关和无关项分列出，得到与时间有关项为

与时间无关项为

与时间无关项为

将方程（3-100）两端的eiωt同时去掉，联合式（3-101），得到两个常微分方程，采用有限元法或有限差分法可以求解y0（z）和yc（z），通过y（z，t）=y0（z）eiωt+yc（z）可得到隔水管动态响应的位移时间历程。

将方程（3-100）两端的eiωt同时去掉，联合式（3-101），得到两个常微分方程，采用有限元法或有限差分法可以求解y0（z）和yc（z），通过y（z，t）=y0（z）eiωt+yc（z）可得到隔水管动态响应的位移时间历程。

如果波浪为随机波浪，则须将波谱离散成N个频率分量，对应的隔水管动态响应为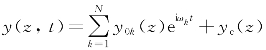，水质点速度为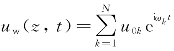。每一个波浪频率对应一个微分方程和一个静态方程，求解各频率分量对应的响应进行叠加即可。

另一种计算理论认为，海流只是隔水管静态分析载荷，隔水管进行动态分析时，只考虑海浪和钻井船运动，无须考虑海流的影响。于是，动态分析时Morison方程仅须考虑隔水管的相对运动，进行一次修正，如下式所示：

如果波浪为随机波浪，则须将波谱离散成N个频率分量，对应的隔水管动态响应为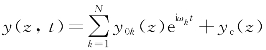，水质点速度为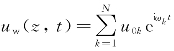。每一个波浪频率对应一个微分方程和一个静态方程，求解各频率分量对应的响应进行叠加即可。

另一种计算理论认为，海流只是隔水管静态分析载荷，隔水管进行动态分析时，只考虑海浪和钻井船运动，无须考虑海流的影响。于是，动态分析时Morison方程仅须考虑隔水管的相对运动，进行一次修正，如下式所示：

两种模型共同之处在于均考虑了隔水管运动的影响。隔水管和钻井船随振荡的波浪一起运动，水质点相对速度减小也就意味着拖曳力的减小。若动态分析考虑隔水管运动，则动态分析相对于静态分析来说，由于后者没有考虑隔水管和钻井船随振荡波浪的运动，自然忽略了拖曳力的变化，造成响应预测偏大。两种模型不同之处在于动态分析时Morison方程的拖曳力项是否包括海流引起的水质点速度，这是两种隔水管动态响应数学模型的唯一差别。

由式（3-101）可知，海流主要形成结构动态响应中的时不变部分。若海流仅仅应用于隔水管静态分析，则对应的隔水管静态分析数学模型应为

两种模型共同之处在于均考虑了隔水管运动的影响。隔水管和钻井船随振荡的波浪一起运动，水质点相对速度减小也就意味着拖曳力的减小。若动态分析考虑隔水管运动，则动态分析相对于静态分析来说，由于后者没有考虑隔水管和钻井船随振荡波浪的运动，自然忽略了拖曳力的变化，造成响应预测偏大。两种模型不同之处在于动态分析时Morison方程的拖曳力项是否包括海流引起的水质点速度，这是两种隔水管动态响应数学模型的唯一差别。

由式（3-101）可知，海流主要形成结构动态响应中的时不变部分。若海流仅仅应用于隔水管静态分析，则对应的隔水管静态分析数学模型应为

比较式（3-101）和式（3-103）可知，海流引起的隔水管动态响应时不变分量不等于隔水管静态分析时海流造成的静态响应。而波浪通过两种方式影响隔水管的设计：通过作用于隔水管的水动力波浪力，通过钻井船的运动响应传递函数影响作为隔水管分析边界条件的钻井船运动。若将海流与海浪分别作为隔水管静态与动态响应的横向载荷，则割裂了波流之间的非线性交互作用，而波流之间的非线性交互对于海洋结构物的设计与分析有着重要影响。存在两种类型的波流非线性交互，取决于海流方向与波浪传播方向相同或者相反，如果海流方向与波浪传播方向相反且海流幅值远远大于波浪幅值时，隔水管将在波浪反方向某个平衡位置附近小幅振动。研究表明，在相同波浪下，海流越大，弯曲应力响应中的静应力越大，不能把波浪与海流联合作用看作分别单独作用下的简单叠加，其主要原因是非线性水动力与水质点相对速度的平方有关。

比较式（3-101）和式（3-103）可知，海流引起的隔水管动态响应时不变分量不等于隔水管静态分析时海流造成的静态响应。而波浪通过两种方式影响隔水管的设计：通过作用于隔水管的水动力波浪力，通过钻井船的运动响应传递函数影响作为隔水管分析边界条件的钻井船运动。若将海流与海浪分别作为隔水管静态与动态响应的横向载荷，则割裂了波流之间的非线性交互作用，而波流之间的非线性交互对于海洋结构物的设计与分析有着重要影响。存在两种类型的波流非线性交互，取决于海流方向与波浪传播方向相同或者相反，如果海流方向与波浪传播方向相反且海流幅值远远大于波浪幅值时，隔水管将在波浪反方向某个平衡位置附近小幅振动。研究表明，在相同波浪下，海流越大，弯曲应力响应中的静应力越大，不能把波浪与海流联合作用看作分别单独作用下的简单叠加，其主要原因是非线性水动力与水质点相对速度的平方有关。