深水钻井顶张力隔水管的数学模型是位于垂直平面内的梁在横向载荷作用下变形的线性常微分方程。取水平方向为隔水管分析坐标系的Y轴，垂直方向为坐标系的Z轴。

梁弯曲变形的四阶常微分方程为

式中　EI——隔水管的抗弯刚度；

p——轴向压力（当p＜0时，p为张力）；

w——隔水管单位长度的总重量；

f——沿水平方向作用于隔水管单位长度上的波流联合力。

由于p沿着隔水管长度方向线性变化，所以任一高度处的轴向压力为

式中　p（0）——隔水管承受的顶张力。

采用Morison方程和Stokes 5阶波浪理论，计算作用在隔水管的准静态环境载荷：

式中　cD——拖曳力系数；

cM——惯性力系数；

ρ——海水的密度；

D——隔水管直径；

u——水质点速度；

——水质点加速度。

隔水管静态变形与应力主要由两类外部条件引起：一类是隔水管顶部随钻井船的初始偏移，另一类是横向的海洋环境载荷。进行静态变形与应力分析时，将钻井船的初始偏移作为隔水管上部顶端的位移边界条件来处理。

可以采用多种方法来计算隔水管的横向变形和应力，如可以忽略抗弯刚度将隔水管蜕变为缆绳进行求解，也可以采用有限差分法，如有限元法、四阶龙格-库塔法、幂级数法等。

隔水管在该截面处所承受的由于轴向载荷所产生的轴向应力为

式中　T——某截面处的张力；

A——隔水管的横截面积。

其中

式中　Ttop——隔水管承受的顶张力；

Wr——在水中隔水管自顶端至临界截面的重量，包括隔水管重量、隔水管附属管线（如截流与压井管线）重量、内部包含物（泥浆、钻杆等）重量以及浸没在水中部分所承受的浮力等。

设隔水管某截面上所承受的弯曲应力为σb，则隔水管凸侧所承受的组合应力为

隔水管凹侧所承受的组合应力为

研究表明，隔水管承受的等效应力、凹凸两侧的组合应力、弯曲应力、弯矩都可作为隔水管设计和安全评估的重要内容。隔水管凹凸两侧的组合应力须通过改变顶张力以施加最优的顶张力，使得隔水管凸侧的最大组合应力小于隔水管材料屈服强度的40%，并使得隔水管凹侧的最小组合应力大于隔水管材料屈服强度的10%，即为海洋钻井隔水管的设计区间，也可以作为隔水管静强度校核的一个方法之一。隔水管三向应力状态分析如图3-6所示。(www.daowen.com)

图3-6　隔水管三向应力状态分析

同时，隔水管还受到径向应力与环向应力的作用，其原因是隔水管的内外静水压力所造成的。外部静水压力是由于海水的静液体压力产生，内部静水压力是由于钻井泥浆的静液体压力、管子中压力波动、油及天然气的异常压力产生。因此，在正常钻井条件下，内部静水压力仅仅由泥浆的静液体压力产生，但是在操作过压（operational overpressure）情况下，内部静水压力是由泥浆的静液体压力和内部压力两者共同产生。因此，任意的隔水管主单元体处于三向应力状态如图3-6所示，三个主应力分别是组合应力（轴向应力+弯曲应力）、环向应力（周向应力）和径向应力。

对厚壁筒而言，由于内外静水压力形成的径向应力与环向应力可由平面问题的极坐标解给出，径向应力σr和环向应力σθ分别为

式中　a、b——分别为隔水管的内外径；

pE、pI——分别为内外静水压力。

由式（3-93）可知，在给定高度处，厚壁筒的径向应力σr和环向应力σθ都是半径r的函数，两者都随着半径变化而变化。对于隔水管这样的薄壁筒（a／b≥0.9）来说，式（3-93）就不再适用。但是，可以认为隔水管环向应力沿壁厚均匀分布，而忽略了径向应力和其他横向剪应力。因此，任意的隔水管主单元体就处于二向应力状态，两个主应力分别是组合应力和环向应力，可按照第四强度理论进行隔水管设计和静强度校核，这可看作隔水管设计和静强度校核的另一种方法。

隔水管水动力学直径（有效直径）也是隔水管分析时的重要因素，一般来说，隔水管水动力学直径要远远大于其实际直径。到目前为止，未见相关文献讨论过该问题。挪威的VIVANA是涡激振动的预测程序，该软件采用“等效体积法”计算水动力学直径，也即将隔水管和附属管线的体积相加，然后以一个虚拟的与隔水管和附属管线体积和相等的圆柱体的直径作为隔水管水动力学直径。采用下式计算平均水动力学直径：

式中　V——全部浸没于海水中的体积；

Lw——浸没于海水中的长度。

另一种方法采用“等效直径法”计算水动力学直径，即将隔水管直径和附属管线直径进行简单相加得到一个直径作为水动力学直径。

于是，对于隔水管水动力学直径，按照垂直于流向的截面的最大外径计算，即

水动力学直径=隔水管直径+节流线直径+压井线直径

对于浮力块隔水管，则演变为

水动力学直径=隔水管浮力块直径+节流线直径+压井线直径

阻力和质量系数主要随横断面形状、粗糙程度、雷诺数、丘里根-卡朋特（Keulegan-Carpenter）数及辅助管线走向等变化。正确选择Cd是确定隔水管状态的主要因素，因为阻力既控制着流体动力激励，又控制着阻尼。超大Cd值的选择也不总是保守的。

一般采用的Cd和Cm值如下：

浮隔水管（根据浮力模块的直径）

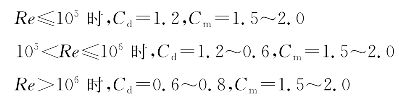
裸隔水管（根据主管直径）

其中，Re指雷诺数。

另外一种情况是在根据相应Cd和Cm值预测出的直径和面积之和的基础上，使用“当量直径”和“当量面积”（隔水管主管加上节流、压井和辅助管线）。

在钻井作业模式下可安全开展所有正常钻井活动，包括继续钻进、起下钻、管下扩眼、循环等。钻井模式下，隔水管的Mises应力必须保持低于2／3的屈服应力，同时需要考虑以下情况：

①隔水管通过伸缩接头和张力器与钻井船相连。

②隔水管内充满最大密度钻井液。

③所有辅助管线承受最大压力。

④主管壁厚考虑5%的制造公差（比公称值减少5%）。

⑤隔水管主管in的腐蚀量。

⑥由于浮力块吸水，其浮力效率降低3%。