（一）按运行时的最大转速求热套件不发生分离时所需的过盈

在电机上采用热套件配合的零部件，大部分是套在轴上的圆环状的零部件，前者称“衬件”，后者称“套件”，如图3-44所示。

显然，套件在受力上处于不利的状况下，故仅计算套件。本节以b=b′为例，其他情况见本章参考文献[5]。

在离心力作用下，套件的内圆及衬件的外圆将分别产生径向“位移”——u₁ω及u′₂ω：

u₁ω=9.8γω²R2³λω1/（gE）（cm）

u′₂ω=9.8γω² R′₂³λω′₂/（gE）（cm） （3-40）

式中γ——材料密度，对钢，取7.85×10³kg/cm³；

ω——旋转角速度（rad/s）；

R₂，R2′——分别为套件的外半径（cm），衬件的外半径（cm）；

g——重力加速度，取g=980cm/s²；

E——钢的弹性模量，碳钢取2.0×10⁷N/cm²；

λ_ω1、λ^′_ω2——套件、衬件的柔度。

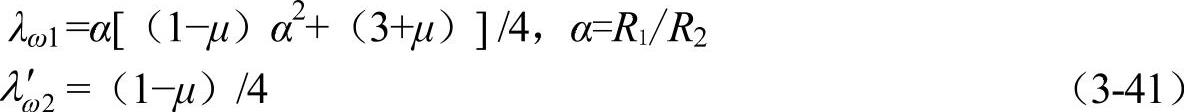
式中，μ为泊松比，对碳钢，取μ=0.24～0.28。

设配合面的接触压强为p，则在压力的单独作用下，使套件内圆产生的径向位移u₁₁为

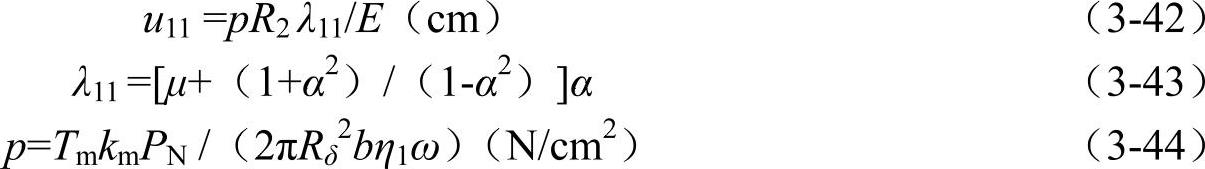
式中R_δ——套件、衬件套在一起后的共同半径（cm），计算时可取R_δ≈R₁或R′₂；

b——衬件宽度（cm）；

η₁——套件、衬件配合面间摩擦系数，它与合面间压强p有关，见图3-45，为安全起

见，可取η1≈0.05；

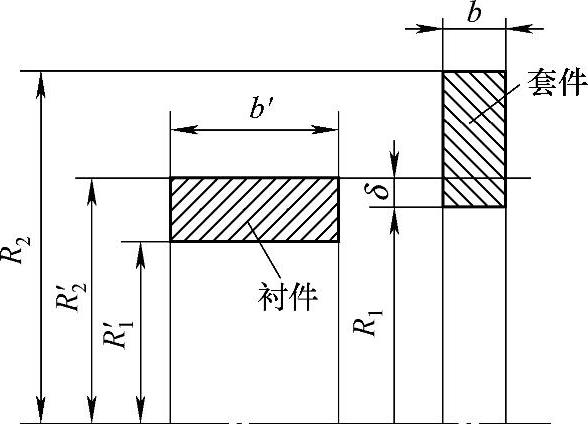
图3-44 环与实心轴过盈配合示意图

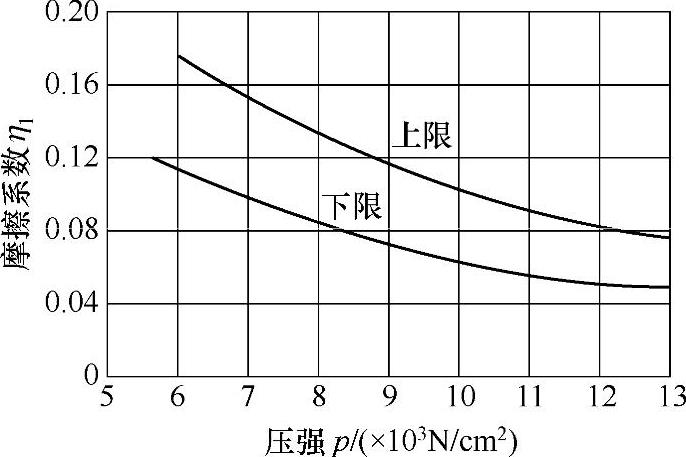
图3-45 套件和衬件之间的摩擦系数与配合面上的压强的关系(www.daowen.com)

注：上限用于计算解开所需的轴向力；下限用于计算配合零件转矩传递最大值。

T_m——电机的最大转矩倍数；

km——摩擦力矩的安全系数，取km≈1.2～1.3；

P_N——电机额定功率（按1kW≈10⁵N·cm/s代入式（3-44））。

衬件外缘的径向位移（受到压缩，方向与u₁₁相反）u′₂₂为

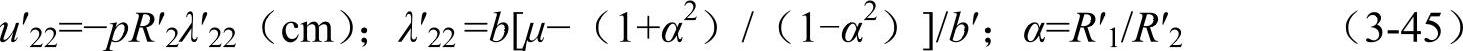
在旋转惯性力和接触压强同时作用下，套件的内缘的径向位移δ₁为

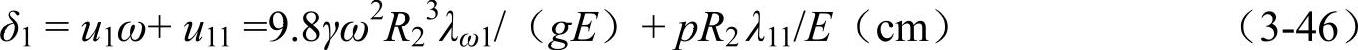
衬件外缘的径向位移−δ₂为

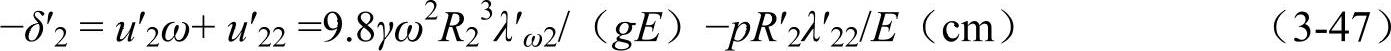
配合公差δ=δ₁+δ′₂=9.8γω²R₂³λω1/（gE）−9.8γω²R′₂³λ′ω2/（gE）+pR₂λ₁₁/E+pR′₂λ′₂₂/E（cm）（3_-48）

设决定配合公差的条件为“松脱转速”ω₀，即在ω=ω₀时，p=0，则配合公差为

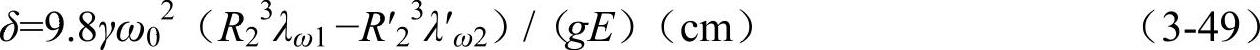
式（3-49）即为按给定的配合公差δ，即所求的在半径方向的过盈量。若要使δ值具有一定的安全裕度，可在ω₀值上考虑：可令ω₀=1.1～1.3n_max，nmax为电机工作时可能出现的最大转速。

将式（3-49）代入式（3-48），解出p：

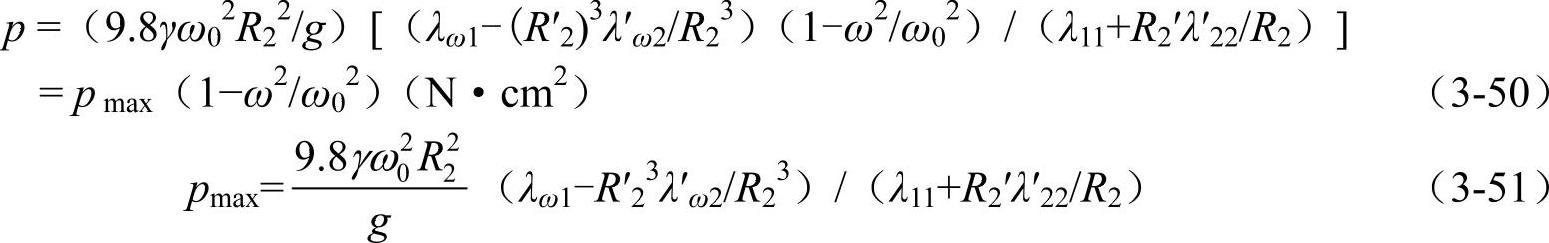
式（3-50）为在给定的ω₀的条件下，计算在各种ω的条件下接触压强的公式，式（3-51）为未转动时的接触压强，它是在各种转速下的最大值。

（二）按所承受的转矩求所需的过盈量

电机产生最大转矩T_m时的角速度ω=ω_m[ωm≈（0.7～0.8）ω_N，ω_N为额定角速度]，将式（3_-44）代入式（3-48）得

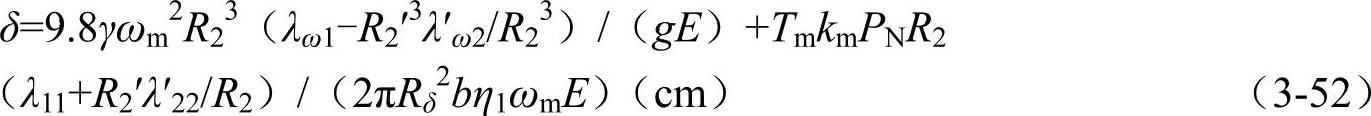
式（3-52）即为传递最大转矩时所需的在半径方向上的过盈量。将式（3-52）和式（3-48）中消去δ，便得出在各种角速度ω下求取接触压强的公式。

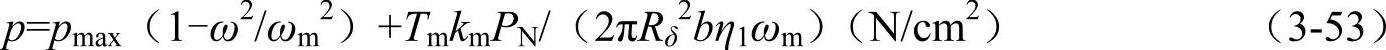
式（3-53）为在不同角速度ω下传递扭矩时的接触压强。其中p_max、Rδ、b及η1的含义及取值与式（3-51）及式（3-44）中的相同。