（一）起动时定、转子绕组温升

以下计算是假定在起动过程中，没有其他能量损失，全部转变为绕组中的热量。

1.定子绕组温升Δθ_Cu1

Δθ_Cu1=F_A（K₁i_stJ1）2K₂t_st（K）（2_-1）

式中K₁=0.84～0.88；

K₂=0.57～0.83，当t_st数值小时，取较大的值，或查图2−29；

F_A可由表2−16查得：

J₁——定子电密（A/mm²）；

t_st——起动时间（s），t_st=J ω/T（s）；

J——电机及负荷转动惯量之和（N·m²）；

ω——角速度，ω=2πn/60；

T——用于起动时的加速转矩（N·m）。

不同的负荷，T值有不同的取法，比如拖动转动惯量较大的离心式风机时，可参照下式

计算T值：

T=[（T_st+T_m）/2+T_L]975P_N/n（N·m）

式中T_st——电机的堵转转矩；

T_m——电机的最大转矩；

T_L——被拖动的设备的阻转转矩，对于离心式风机可取T_L=0.41T_N。

式中的转矩均为标幺值。

2.转子绕组温升Δ θ_Cu2

Δθ_Cu2=AV₂K₃/（cm_Cu2）（K）（2_-2）

表2-16 与不同的定子绕组温升θ₁（K）对应的F_A值

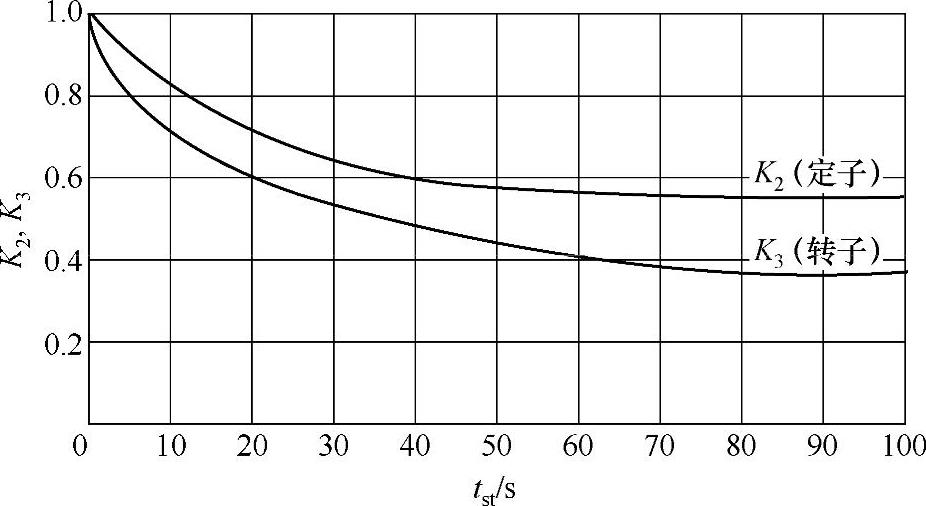
图2-29 起动温升计算修正系数

式中m_Cu2——转子绕组质量（kg）；

K₃=0.37～0.71，当T_st数值小时，取较大的值，或查图2−29。

AV₂=GD² n₁²T_Mav/（7300T_Gav）（W·S）（2−3）

式中GD²——电机与负荷GD²飞轮力矩之和（N·m²）；

T_Mav、T_Gav——电机与负荷等效转矩（N·m）。

其含义是：在额定转速范围内，与电机及负荷T-s曲线所包容的面积分别相等的矩形面

积的纵坐标的高（横坐标一律为n_N）

（二）满负荷稳定状态下的电机温升

满负荷稳定状态下电机的温升，即定子绕组的温升θ₁。

1.将定子作为均匀发热体时电机表面温升θ_S的表达式定子可以视为一均匀发热的物体，当发热与散热在某一温度下达到平衡状态时，电机表

面温升θ_S可用下式表示：

式中Q——稳态时单位时间所产生的热量（W）；

Α——定子表面的传热系数（W/（cm²·K）），见表2-17；

S——定子表面面积（cm²）。

表2-17 表面传热系数

式（2-4）表明：无外风扇的电机的表面温升与定子产生的热量成正比，与散热系数、散热面积成反比。其中散热系数a与电机表面状况有关，电机在使用中若表面有灰尘、污垢，使a变小，从而使温升增高。

2.计入定子本身散热途径中各部分温度降低之后的定子绕组温升

空气冷却后的电机的散热主要由两大途径（固体之间与固体与气体之间）构成。

（1）固体之间温度降

固体之间温度粗略地可以看成由两部分组成——绝缘层中（包括浸漆及漆膜）及铁心中（机座与铁心可视为一体）。

1）绝缘层中的温度降θ_i。

(www.daowen.com)

式中Q——由绕组产生并经绝缘传出的热量（W）；

δ_i——绝缘层厚度（cm）；

S——绝缘部分散热面积（cm²）；

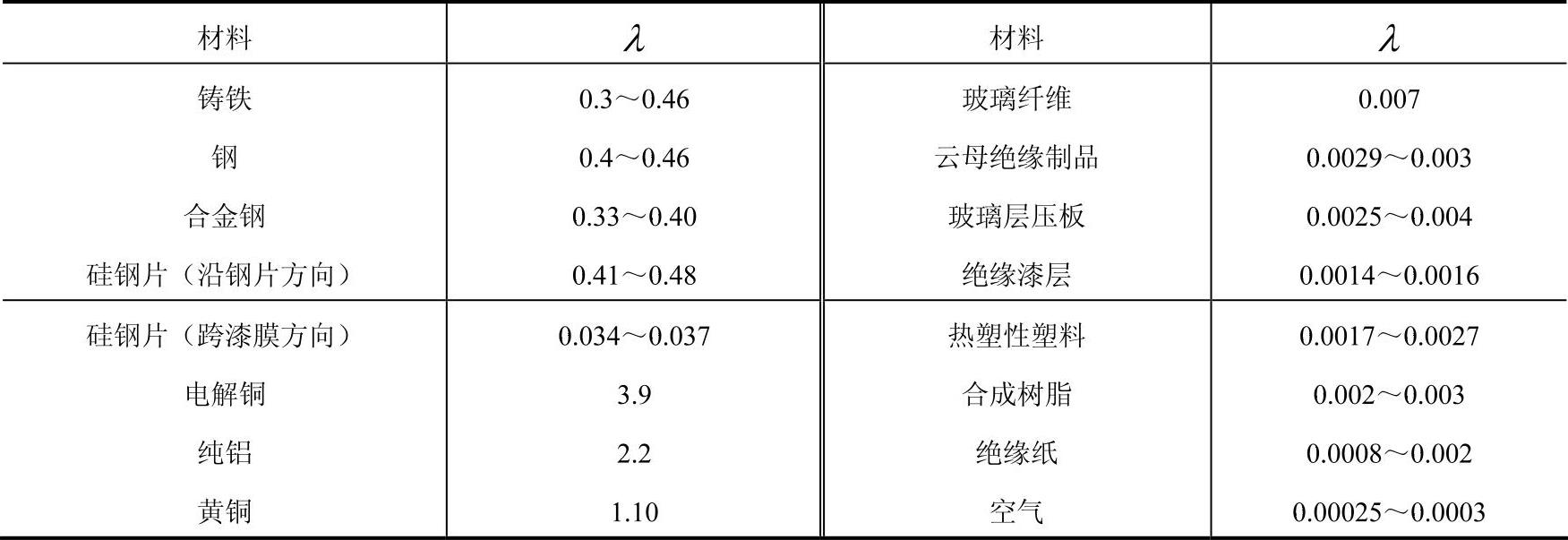
λ——热导率（W/（K·cm）），见表2-18。

表2-18 电机常用材料及空气的热导率λ（单位：W/（K·cm））

将公式中的Q用相应部分的定子铜耗P_Cu1（W）带入，即为该处绝缘层中的温度降。如计算槽部：

若计算端部：

式中l——铁心长（cm）；

l_c——半匝线圈平均长（cm）；

l_E——半匝线圈端部平均长（cm）。

计算时，若槽部δ_i、S、λ与端部的不同，则代入θ_i公式时应分别取值。

2）铁心表面的平均温升θ_Fe。

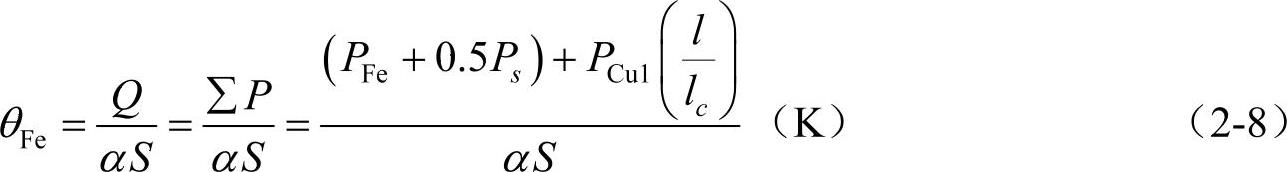
式中S——定子铁心内圆面积，S=πD_i1 l（cm²）；

P_Fe——铁耗（W）；

P_s——电机杂散损耗（W）；

P_Cu1——定子铜耗（W）。

（2）绕组端部表面对空气的温升θ_e

式中P_e——端部绕组铜耗，P_e=P_Cu1l_e/ l_c （W）；

α_e——端部表面散热系数；

S_e——端部绕组表面积，S_e=L₁l_EZ₁ （cm²），L₁为绝缘线圈断面的外缘周长（cm）。

（3）定子绕组温升θ₁

θ₁=θ_CuFl+θ_CuElE/（l+l_E） （K）（2-10）

式中θ_CuF——绕组有效部分温升，θ_{Cu F}=θ_Fe+θ_i （K）；

θ_CuE——绕组端部温升，θ_CuE=θ_e +θ_i （K）。

3.计入转子辐射热之后的定子绕组温升

转子对定子的热辐射对定子绕组的温升θ₁有一定影响，尤其对冷却方式为IC0141的封闭式电机，这已为实践所验证，但目前国内有关电机设计方面的书籍上，在计算θ₁时均未将转子的热辐射计入，这是θ₁的计算值与试验值间误差较大的原因之一。德国西门子公司将转子热辐射（用计入转子铜耗P_Cu2来考虑）计入后经试验修正得出以下θ₁的计算公式。

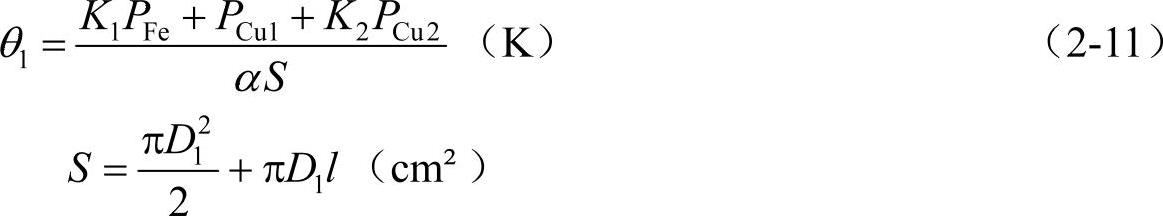
式中α——用定子温升实测值统计数据按上式反算后求得的经验系数（W/（K·cm））；

D₁——定子铁心外径（cm）；

l——铁心长（计及通风沟）（cm²）；

K₁、K₂——经热路计算及试验获得的修正系数。

将三种损耗（其中P_Fe为总铁耗）均纳入θ₁的表达式之中是符合实际情况的。K₁、K₂是

与电机结构、工厂采取的制造工艺均有关的系数，当将K₁、K₂及α在典型结构上经过修正确定下来之后，用该公式计算同类产品的其他规格时，算得的θ₁与试验值之间的误差就很小。

（三）对温升的分析、估算

因目前国内尚无与试验结果比较吻合的温升（指θ₁）计算公式，所以异步电机的设计人员基本上都是用分析、估算的办法确定所设计产品的温升。

分析、估算的办法是：将所设计的产品的电磁负荷、热负荷及散热面积与已有试验结果的同类产品相比较。其中定、转子电密J₁、J₂，因温升与它们的二次方成正比，对θ₁影响较大。若所参照的产品的θ₁较高或较低，可用上述的二次方关系调整所设计产品的J₁、J₂。定、转子负荷A₁、A₂与θ₁成一次方的比例关系；B_δ则随产品类型的不同有一定的选择范围，不宜大幅度地增、减。

除上述的规律外，在借助于分析、估算确定所设计的电机的方案时，还应注意以下几点。

1）在系列产品设计时，为保证“系列性”，个别规格的电磁负荷会选得较低或略偏高。

2）应注意工艺上对θ₁有影响的因素，如浸渍方法和铁心加工水平等。

3）注意电磁负荷分配的合理性。

4）注意散热面积，在同一机座号的不同长度电机中，若P_N1＞P_N2，且采用IC0141的散热方式，应使l₁/l₂略大于P_N1＞P_N2，即散热面积的增加幅度应略大于功率的增加幅度，否则应降低电磁负荷、热负荷。

5）θ₁应按工厂的具体情况留有一定的裕度，对于新设计的待定型的产品，至少应留有10K的裕度。

尽管温升计算有误差，有时还比较大，但对于一个全新产品来说，仍可以得到有参考价值的温升的粗略计算值；另外，还可以从公式中寻求降低温升的途径。若式（2-11）中的系数K₁、K₂及α经过多次试验得到比较切合企业实际情况的数值，则式（2-11）就具有较高的参考价值。