双目传感器测量原理是利用空间同一点在两摄像机面上的视差大小计算空间点的三维坐标，要完成空间坐标点的测量，首先必须确知空间点在两像面上的像点坐标，此两像点称为匹配像点。在实际测量中，要从获得的左右摄像机的像面图像恢复空间点的三维坐标，必须在两幅图像中找到匹配的像点坐标，这一过程被称为特征点匹配。以往的文献资料所介绍的双目传感器多为正直摆放姿态，即两光轴相互平行。这种双目传感器结构简单、分析简便，其外极线共线且与像面水平轴平行，但在测量精度较高的近距离处其可测尺寸较小。对于精密检测任务，则需要采用交向摆放姿态的双目传感器，即两光轴不平行，且允许两像面之间存在旋转。这样不仅有利于近距离高精度测量，而且还可降低对传感器安装精度的要求，从而可降低成本。

图2 交向摆放姿态的双目模型示意图

图2所示为一交向摆放姿态的双目模型示意图，空间任意测点P与左右透视中心O_a、O_b构成一个平面，称为外极平面（epipolou）。外极平面与左右像面相交形成左右两条外极线（epipolar lines）。对于正直摆放的双目模型，所有外极线都是平行于像面水平轴的，即所有外极线相交于无穷远。对于交向摆放的双目模型，每一像面上的外极线都相交于一点，即外极中心。

设双目传感器中左右摄像机坐标系相互变换关系为

x_a=X_as；y_a=Y_as；z_a=f_as （2）

式中，f_a为左摄像机有效焦距。将此射线转换到右摄像机坐标系，得

若右摄像机有效焦距为f_b，则有

存在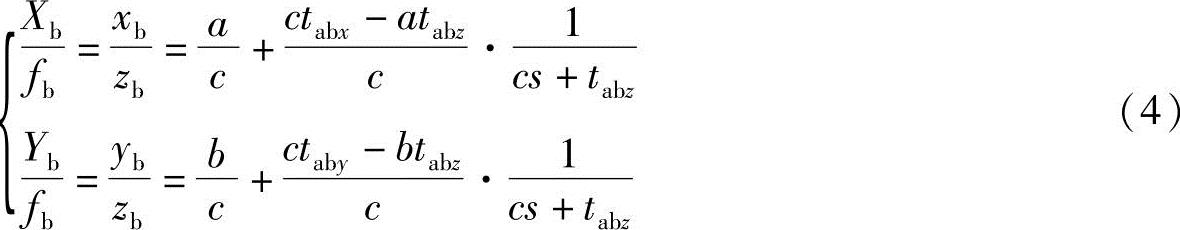

式（4）表示右像面上的一条线段。此线段从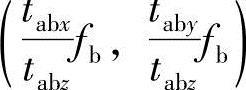点（即s=0点）到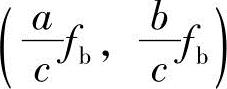点（即s=∞点）。由此可见，左像面上任意一点与右像面上一条线段相对应。s=0点为左摄像机透视中心O_a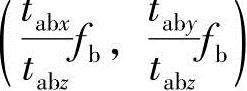，点是其在右像面上的投影点，即右外极中心EC_b。V_pb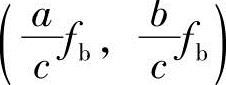点对应于射线（2）的无穷远点（即s=∞点）。(www.daowen.com)

同理，右像面上任意一点与左像面上的一条线段相对应。右摄像机透视中心O_b在左像面上的投影点为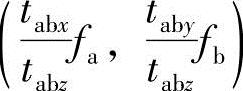，即左外极中心EC_a。

由外极约束理论不难发现，左像面上一条斜率为k_a并通过EC_a点的直线应与右像面上一条斜率为k_b并通过EC_b点的直线相匹配。实际上，这两条直线分别为同一外极平面与左右像面的交线。由此可见，如果将左右像面像点坐标转化为以EC_a和EC_b为原点的极坐标，则可利用其极角和极径很容易找到各自的匹配点，从而可以大大简化匹配过程。

定义k_a和k_b分别为同一外极平面内左右外极线的斜率，称其为外极斜率，二者互为外极匹配斜率。经推导可得k_a、k_b相互转换关系如下：

对于空间棱线或投射到物体表面的单光条，测量时首先将其摆放成便于检测的姿态，然后利用式（5）和式（6）很容易完成匹配过程。因为空间直线在像面上的投影仍然是直线，所以直线的检测既可以用两面相交法，也可以用上述的外极斜率匹配法先求空间离散点，然后再进行直线拟合。对于单光条的检测，由于物体表面变化不同，因而光条的弯曲程度也不同，光条在像面上的投影不易用某一确定的方程来表达，此时外极斜率匹配法在光条检测方面就显示出明显的优越性。

由于CCD输出的是离散图像，左右像面上的离散特征点可能在对方像面上没有现成的匹配点，这样就需要进行插值计算。首先算出两像面特征点的外极斜率值k_ai和k_bi，然后再算出对应于k_ai的外极匹配斜率k′_bi和对应于k_bi的外极匹配斜率k′_ai。由于像面匹配特征为单光条，并且光条是连续的，所以可以用下述插值方法计算匹配点坐标。设k′_bi介于k_bi-1和k_bi之间，那么左像面内斜率为k_ai的点在右像面内的匹配点的像面坐标为

同理，若k′_ai介于k_ai和k_ai+1之间，则右像面内斜率为k_bi的点在左像面内的匹配点的像面坐标为

这样在进行空间直线或曲线拟合时，拟合点数便多了一倍，从而提高了拟合精度。最后利用左右摄像机与世界坐标系之间的关系可得到4个线性方程，通过最小二乘法解方程组可得光条世界坐标值。由于大大缩小了匹配搜索范围，因此匹配速度显著提高。

由于CCD像面尺寸有限，并且外极中心EC_a和EC_b不会偏离像面水平轴很远，所以两像面特征点的外极角不会接近90°，从而不必担心由于外极斜率过大而带来的误差。