摄像机成像系统并非理想的成像系统，存在镜头畸变；此外，像面接收器件是CCD阵列，是由一个个像元排列组成的，像元间距存在误差，况且光轴与像面的交点不一定在像面中心，且光轴与像面有垂直度误差。CCD驱动信号经采集卡采样，水平像元的等效间距也要发生变化等。考虑到这些实际因素，建立如下摄像机实际模型（将像元间距分散性误差合并到畸变中）。

图1 摄像机模型

如图1所示，在像平面上，离散的像素坐标系为O_RI_xI_y，I_x取水平像元阵列方向，I_y取垂直像元阵列方向；设O为透视点，作Oz轴垂直像面，交像面于O_I点，Oz轴方向取OO_I方向；过O点作Oy轴平行于I_y轴，且方向与I_y一致，再按右手法则确定出Ox轴。从而获得了摄像机坐标系Oxyz；在像平面上以O_I为原点作O_IX轴平行于Ox轴，且方向一致，作O_IY轴平行于Oy轴且方向一致，显然O_IY轴也与I_y轴平行。从而得到正交的理想像面坐标系O_IXY。

O_RI_xI_y以像素作度量单位，设垂直像素间距的实际值为W_y，水平像素间距经采样后的实际值为W_x，则I_x轴度量单位为W_x，I_y轴度量单位为W_y。图像的水平像素间距W_x一般不与CCD的加工尺寸一致，它与CCD的驱动频率及图像采集卡的采样频率有关。W_x的真值常需在标定过程中确定。设计算处理时使用了W_x的近似值W_ex，令s_x0=W_ex/W_y，s_x=W_x/W_ex，则Wx=s_xs_x0W_y。

为讨论方便，以O_R为原点建立一新坐标系O_RX_EY_E，坐标系方向与O_RI_xI_y完全相同，只是坐标轴当量已经过预校正，满足如下关系

X_E=s_x0W_yI_x；Y_E=W_yI_y （1）

从而有

X=s_x（X_E-C_1XE）；Y=Y_E-C_1YE （2）

式中，（C_1XE，C_1YE）为OI点在O_RX_EY_E中的坐标。

由此可以看出，摄像机的内部几保结构参数可用f、s_x、s_x0、W_y及O_I在O_RX_EY_E中的坐标（C_1XE，C_1YE）来表征。(www.daowen.com)

设世界坐标系为O_wx_wy_wz_w，且为右手直角坐标系，则摄像机坐标系相对世界坐标系的位置可用下式表示

由透视变换理论可得如下变换关系（带u下标表示不考虑畸变时的坐标）

由式（2）、式（3）和式（4）可推得

至此，建立了不考虑畸变时的摄像机几何模型。考虑摄像机畸变影响时，空间点在像面上的实际成像位置与理想位置不一致，设空间点P（x_w，y_w，z_w），经摄像机成像，不考虑畸变时的理想像点位置（相对于O_RX_EY_E坐标系）为P_Eu（X_Eu，Y_Eu），考虑到畸变影响时实际成像位置为P_Ed（X_Ed，Y_Ed）。一般地，P_Eu、P_Ed之间的相互位置关系可用一畸变函数来描述（带d下标表示考虑畸变时的坐标）。下面介绍两种常用的摄像机畸变模型。

（1）只考虑径向畸变误差的径向畸变模型

设径向畸变中心在坐标系O_RX_EY_E坐标为（C_dXE，C_dYE），有如下关系

其中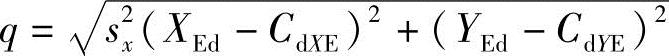，，称k₁、k₂、…为径向畸变系数。

（2）考虑径向及切向畸变的畸变误差模型

称p₁、p₂为切向畸变系数。