前面提到通过两台经纬仪互瞄和测量一参考尺度，再通过空间解析计算求得两经纬仪的相互位置关系。实际上这就是确定R和T的过程。它是通过调水平后互瞄使得R=E，T_z=0，即两经纬仪之间只存在纯平移关系，该过程是人为调整的过程；再对一已知精确长度值的基准标尺进行测量反算出T_x=b，T_y=h，这时T=（bh 0）^T。只要将此R、T值代入式（8），并将像面坐标值改为角度值就可得到传统的空间前方交会模型。因此，我们可认为传统的数学模型是所建立的新模型的特例。下面讨论一般过程的R和T值的确定。

从式（8）中我们得到

（T_x-X_bT_z）[Y_b（r₇X_a+r₈Y_a+r₉）-（r₄X_a+r₅Y_a+r₆）]

=（T_y-Y_bT_z）[X_b（r₇X_a+r₈Y_a+r₉）-（r₁X_a+r₂Y_a+r₃）] （9）

式（9）是一个含有12个未知数T_x、T_y、T_z及r₁、r₂、r₃、r₄、r₅、r₆、r₇、r₈、r₉的非线性方程。对T_x、T_y、T_z而言它是齐次的。所以，我们只能求得含有比例因子的T。在求得T（含有比例因子）和R以后，可利用式（8）对每个观测点求得带有比例因子的z_wi。

设T′=αT，根据坐标系的选择法可知T_x≠0，我们选择α=1/T_x。于是有

T′=（1 T_y′ T_z′）^T （10）

这样，式（10）可认为是一个含有11个未知数T_y′、T_z′及r₁、r₂、r₃、r₄、r₅、r₆、r₇、r₈、r₉的非线性方程，用函数f（x）=0来描述，其中

x=（T_y′，T_z′，r₁，r₂，r₃，r₄，r₅，r₆，r₇，r₈，r₉）

另外，r₁～r₉构成的旋转矩阵R是正交的，因而具有六个正交约束条件并由此可构造如下罚函数

其中，M₁～M₆为罚因子，从而得到无约束最优目标函数为(www.daowen.com)

最后可用牛顿—高斯法求解出x。

由式（8）不难求出

或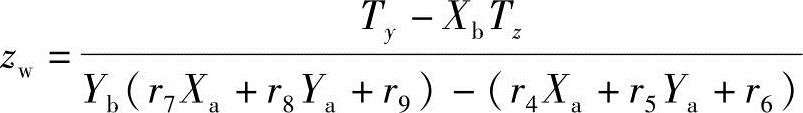

对于P_i点的空间位置分别为（x_wi，y_wi，z_wi）、（x_bi，y_bi，z_bi），对应的像面坐标分别为（X_ai，Y_ai）、（X_bi，Y_bi），其间的关系已描述过。因此，根据透视投影特点，我们可将空间点P_i、P_j间的距离D_ij表示为

（z_wiX_ai-z_wjX_aj）²+（z_wiY_ai-z_wjY_aj）²+（z_wi-z_wj）²=D²_ij （13）前面提到，我们只能先求得带有比例因子的z_w，即z_w′=αz_w。则式（13）可改写为

（z′_wiX_ai-z′_wjX_aj）²+（z′_wiY_ai-z′_wjY_aj）²+（z′_wi-z′_wj）²=α²D²_ij （14）

一旦x已知，根据任两点间的已知距离值D_ij就可由下式求得比例因子α，即

比例因子符号α由坐标选择法决定。这样平移矢量T可由下式确定

至此我们确定出旋转矩阵R和平移矢量T。