采用一种新方法——“微分标定法”进行标定。该方法与Chen^[2]和Agin^[3]所用的方法相比简便易行。

用图4所示的标准块进行标定。已知尺寸如图所示，上下平面距离为ΔZ_g。

将标准块置于二维工作台上，根据视觉检测原理，用P_k光切面可测得与X_g轴平行的两棱线X_go和X_g在像面CCD上的坐标为Y₁₀、Y₁，从而可得与已知量ΔY_g相应的像面上增量ΔY₁=（Y₁-Y₁₀）。

再用P_k光平面切于标准块（图5虚线位置）与Y_g轴平行的棱线X_go上，它在像面CCD上的坐标为X₁₀；然后将标准块右移至实线位置，使P_k与X_g棱线重合，X_g在像面CCD上的坐标为X₁，标准块的移动量δ_x可从二维工作台上读出。

图4 标准块

a）透视图 b）俯视图

图5 用标准块标定

根据式（1）X_g的表达式，标准块移动前后，在像面CCD上的增量为ΔX_i=X₁-X₁₀，在O_gX_gY_gZ_g坐标系中，相应的增量ΔX_g为

ΔX_g=X_go-X_g=S₂-δ_x

由图中几何关系可得出θ_k角

上式与式（1）中Z_g的微分表示类似，在实际应用中，常用差分代替微分，重写式（1）为

a=（D_gp-D_gc）cosβ_k-f+D_pccosβ_k

b=f（D_gpsinβ_k-D_gcsinβ_k-D_pccosβ_k）

c=cosβ_kcosθ_k+sinβ_k

d=f（sinβ_kcotθ_k-cosβ_k）

u=D_gc-D_gp+D_pccotβ_k-f（sinβ_kcotθ_k-cosβ_k）(www.daowen.com)

由式（2）中Y_g的表达式得

因X_g与X₁为非线性，不能直接求微商，因此用增量表示

而ab-bc=fu，则

设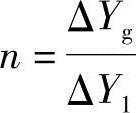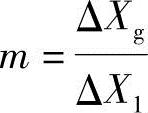，，则上式可变为

m（X₁₀c+d）=fn

将c、d表达式代入上式得

设l=cotθ_k，p=lX₁₀-f，q=X₁₀+fl，代入上式并整理，可得tanβ_k的显式表达式

传感器的5个参数，θ_k和β_k已解出，还剩下D_gp、D_gc和D_pc未知。测得D_gp值（由理论计算和实验证明，该参数的精度要求不高，误差在±5mm内即可）。由图5中的几何关系知

由式（2）得

解由式（3）和式（4）组成的联立方程得

A=fsinβ_k+X₁₀cosβ_k

B=fcosβ_k-X₁₀sinβ_k

E₁=fD_gpsinβ_k-X_go（X₁₀c+d）+X₁₀（D_gpcosβ_k-f）

E₂=D_gp+f（lsinβ_k-cosβ_k）+n（X₁₀c+d）