火箭喷出的超声速流在导流系统底部产生正冲激波，造成激波后的局部高压，势必有部分高温燃气流反吹，使火箭处于高温状态中，这对火箭及整个发射系统来说是非常危险的。因此，必须采取强有效的消防措施来降低火箭箭体的温度，以确保火箭整个发射系统的安全。在发射台周围布置喷水系统最初是以消防为主要目的，在紧急关机和火箭起飞后对发射台和箭体进行冷却降温，将喷水过程扩展到新型大推力火箭发射过程中，可以有效应对发动机工作时造成的极端工作环境，实现对发射台和导流槽的热防护任务。然而，目前国内外对火箭燃气射流喷水的研究还主要集中在抑制超压和降噪方面，对喷水冷却热防护的研究却很少。本书专门就超声速射流中的喷水两相流问题进行理论研究，为运载火箭发射场导流槽的设计和应用提供有价值的参考。

向燃气流场中注水是一种性价比较高的降温手段，早已应用于欧美各种大小型发射场，而注水对火箭发动机尾焰流场所产生的影响鲜见详细报道。Giordan 等通过使用商业软件Fluent 对欧洲航天局的Ariane 火箭发射的不同工况下的注水效果进行仿真模拟，对注水的降温防护效果进行了比较分析。Miller 等通过多组试验来分析注水的降温效果，确定了燃气与水的动量之比对热通量的影响。而国内尚未见公开发表的文献。燃气射流与水的作用是一个非常复杂的两相流问题，仅从理论研究出发不能得出令人满意的答案，存在以下几个疑问：首先是注入的水射流能否进入燃气主流，如果能进入，需要什么样的条件；其次，注水如果能进入燃气主流，是否能达到降温的目的，如果能降温，其降温机理是什么，是否会出现水流反弹现象，从而影响降温效果；最后，也是最关注的就是是否存在最优的参数组合达到最佳降温效果。而下文进行的研究将对这些疑问进行解答。

许多设计参数影响注水的降温效果，包括水/气质量流率之比、轴向注水位置、注水角度、喷头数量、注水方式（柱状或者雾状）、水流速度以及水温等。而这些影响因素很多是耦合在一起共同发挥作用的，要想将这些影响因素完全研究清楚需要大量的针对性试验和数值仿真。而本部分的研究结果主要针对发射场工程应用，因为注水位置受到发射场各种地面设备布置的限制，而注水角度的选择还需要兼顾降噪效果。因此，本部分并不就注水位置和注水角度的影响进行研究，此外，为了便于注水的工程实现，一般采用常温水进行降温，而喷头注水方式也一般采用柱状，因此这两个因素在本部分也视为常量。

本部分主要针对水质量流率m˙w （本部分所有的试验、仿真所用的发动机为相同发动机，其各种燃气参数完全一致，包括燃气秒流量m˙g ，因此改变水的质量流率则改变了水/气质量流率比k）、喷头数量n、水流速度v、喷头出口截面积s 这四个因素对注水降温效果进行研究。而以上几个因素并不是相互独立的影响因子，其中=ρw · s · v ·n 。在常温常压下水的密度是一定的，因此所研究的四个因素只需确定其中三个即可。通常情况下，如果一个研究对象的影响因素有多种，为了研究各种因素各自的效应，需要进行单一变量法研究；而本部分所研究的这四个因素并不完全独立，因此采用保持两个因素不变、改变另外两个因素的双变量法。

降温效果主要体现在以下这些方面：降低射流轴线温度、降低地面温度和减少烧蚀现象等。除了这些方面之外，为了更好地理解注水降温的机理，需要对注水燃气复杂两相流场进行深入分析。因此，本部分还将对流场迹线分布概况、沿轴线等距截面及对称面等进行研究，旨在得到可说明注水降温机理的流场形态特征。

首先，对迹线分布图的物理含义进行解释，该图显示从某一出口流出的所有粒子（流体微团）的主要流场迹线分布。需要指出的是在水射流从喷管出口到底板的流动过程中发生了汽化现象，而该现象并不影响其迹线分布。也就是说，当其温度高于饱和温度时，原来的液态粒子就变成了气态粒子，但其相变过程在迹线图中无法体现。需要指出的是，本部分所用的流场迹线分布图左侧显示的均为温度范围，单位为K；所有温度云图的单位也都为K。

利用燃气流、冷却水及水蒸气共同作用的气液两相仿真模型，建立流场计算模型，通过数值模拟，研究混合流场分布情况，从而研究冷却水降温效果。本部分采用有限体积法来离散控制方程，湍流模型选用RNG k−ε 模型，壁面附近采用标准壁面函数。气液两相流模型采用耦合了液态水汽化方程的Mixture 多相流计算模型。通过非定常算法计算各个时间步内流场分布，直到流场稳定。

1. 几何模型及初边条件

以双水管注水工况为例，计算域示意图如图5.25 所示。坐标原点O 为喷管出口中心，X轴为发动机射流轴线，XOY 平面为水管所在平面，XOZ 平面为无水管平面。需要说明的是如果水管数量变为4，则在XOZ 平面上再添加一组水管即可。计算域共包含两个入口和一个出口，喷管出口为燃气相入口，水管出口为水相入口，计算域外边界则为出口。从喷管出口至地面距离为1.76 m，注水的交汇点为距喷管出口0.26 m 处，注水方向与发动机轴线夹角为60°。根据对称性选取1/4 面对称三维计算域进行计算（图5.25）。边界条件设置见表5.4，其具体位置如图5.26 所示。

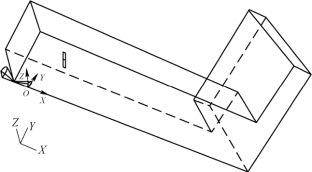
图5.25　计算域示意图

图5.26　边界条件示意图

表5.4　边界条件设置

1） 初始条件

在进行数值模拟之前，必须对流场进行初始化，即给定流场的初始条件。本次计算中，喷管以外计算区域的初始流场取静止大气的参数：P = 101 325 Pa，T = 300 K，V = 0 m/s；初始情况下只有水管出口内有液态水存在，且体积分数为1；喷管内初始条件为：P = 7 MPa，T = 3 000 K。

2） 压力入口边界条件

压力入口边界条件即发动机喷管入口处的条件，由于不考虑点火瞬间的压力攀升过程，发动机的燃烧室压力基本保持恒定，所以压力入口条件为：P0 = 7 MPa，T0 = 3 000 K。

3） 质量入口边界条件

质量入口（mass-inlet）边界条件即水管入口处的条件，根据本部分各种工况下的注水量的不同而不同。

4） 对称面边界条件

由于计算域关于XOY 平面和XOZ 平面均对称，为了减少计算量，则将这两个面都设置为对称面边界条件，这样可以将计算网格数降低为无对称边界条件下的1/4。

5） 壁面边界条件

在数值模拟的过程中，喷管壁面、水管壁面、地面等固壁处采用壁面边界条件。壁面边界条件中，物面边界采用无滑移壁面和绝热壁面边界条件，近壁面湍流计算采用标准壁面函数法处理。(www.daowen.com)

6） 压力出口边界条件

压力出口边界条件即周围环境的条件，设为常温常压，位于计算域的外围。Pout = 101 325 Pa，Tout = 300 K。

2. 计算工况

由于=ρw · s · v ·n 中m˙ w、s、v、n 这四个影响因子并不完全独立，因此采用保持两个因素不变、改变另外两个因素的双变量法。在工程实际应用中最为关心的是下面几种情况。

（1）当水的流量m˙w 和水管数量n 已经固定，是否可以通过调整单个水管出口截面积s 来调整流速v，从而达到优化降温效果的目的。

（2）当水流速度v 和水管数量n 已经固定，是否可以通过增大单个水管出口截面积s 来增大流量wm˙ ，从而达到优化降温效果的目的。

（3）当水流速度v 和单个水管出口截面积s 已经固定，是否可以通过增加水管数量n 来增大流量wm˙ ，从而达到优化降温效果的目的。

（4）当单个水管出口截面积s 和水管数量n 已经固定，是否可以通过提高出口速度v 来增大流量wm˙ ，从而达到优化降温效果的目的。

根据所关心情况并且本着最大限度利用所设置的工况进行多组对比将八种工况设置如下，分为4 组，分别进行对比，见表5.5～表5.8。下面将分别对这几组工况展开详细研究，需要说明的是，如某些个别工况是几组中同时包含的，将不再重复介绍。

表5.5　水的流量与水管数量固定条件下各个工况

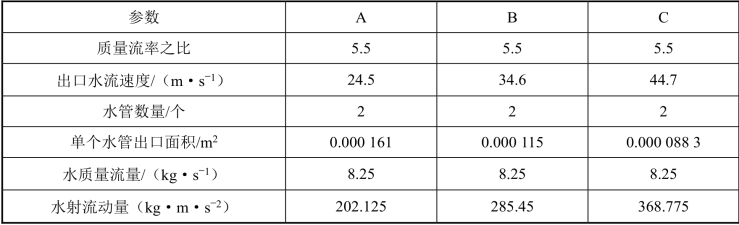
表5.6　水的流速与水管数量固定条件下各个工况

表5.7　单个水管出口截面积与水的流速固定条件下各个工况

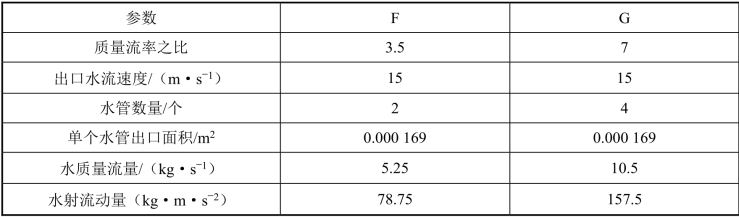
表5.8　单个水管出口截面积与水管数量固定条件下各个工况

续表

此外，作为各种注水工况的对比工况，对无水自由射流工况下的流场也进行了计算。无水自由射流工况下流场迹线图如图5.27 所示，图5.28 显示的是轴线上距喷管出口距离为0.1～1.3 m、间距为0.1 m 的13 个截面上燃气射流分布温度云图。而其他计算结果会在与其他工况的比较中列出。燃气流量约为1.5 kg/s，出口速度约为2 000 m/s，则燃气主流的动量为 =3 000 kg ·m/s2。

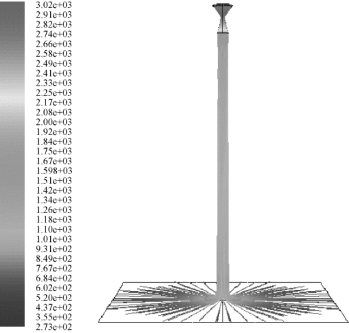
图5.27　无水自由射流工况下流场迹线图

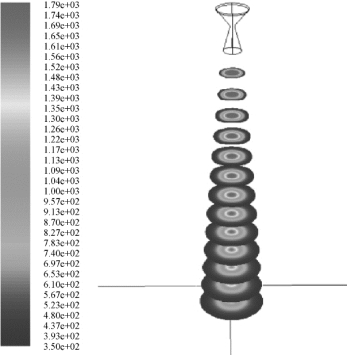
图5.28　截面温度云图（X = 0.1，0.2，⋅⋅⋅，1.3）