如前所述，燃气射流通常是超声速的高速流动，不存在清晰的流动分层，流线也不再清楚可辨，这种流动状态被称为湍流。层流与湍流的流线如图4.31 所示，湍流中存在多个尺度的涡以及由此产生的较强的质量、动量和能量交换。

对于燃气射流动力学问题，湍流的时间与空间尺度远小于几何模型的特征尺寸，要想完全求解其各个时空尺度的流动结构，必须确保数值计算的时间与空间尺度足够小，这对计算资源的要求极高。另外，实际工程中往往更为关注燃气射流流场的时均特性。因此，人们寻求一种不需要解析湍流流动细节而又能够反映湍流对流场时均量的影响的方法。目前常用的方法是对NS 方程做Reynolds 平均或Favre 平均，前者常用于求解不可压缩湍流，后者则用于可压缩湍流。严格来讲，燃气射流中的湍流属于可压缩湍流。但可压缩湍流的计算较为复杂，且工程中燃气射流的湍流可压缩效应影响的区域集中在核心区附近的高速区域，在其余流场则可近似为不可压缩湍流。因此，射流仿真中常用的是雷诺平均（Reynolds-average）湍流模型［6］。

1. Reynolds 平均

为了反映湍流的时均特性，雷诺提出，将流场中的瞬态量φ 写成时均量φ 与脉动量φ′之和，即

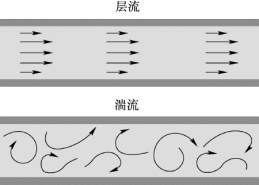
图4.31　层流与湍流的流线

其中，时均量定义为

对质量方程与动量方程中的速度取雷诺平均可得

2. Boussinesq 假设

为了闭合RANS 方程，Boussinesq 假设湍流对平均流的作用仅相当于增大了扩散系数。对于动量方程而言，相当于增大了流体的黏性，且湍流黏性是各向同性的，即

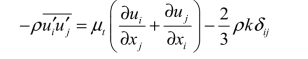
其中， tμ 为湍流黏性；k 为湍流动能。通过Boussinesq 假设，RANS 方程中多余未知量由6个（三维）变为2 个。为了使整个方程组封闭，需要进一步构建关于湍流黏性与湍流动能的方程。通过这一过程建立的方程即所谓的湍流模型。

需要注意的是，Boussinesq 当时提出该假设是基于物理直觉的，并没有严谨的理论支撑。随着对湍流研究的逐渐深入，人们逐渐认识到Boussinesq 假设的各向同性湍流黏性与实际湍流流动并不吻合。在射流冲击传热等各向异性较强的问题上，Boussinesq 假设得到的传热速率与试验结果存在明显的出入。尽管如此，由于Boussinesq 假设形式紧致，计算结果稳定，并且对于大多数问题能够得到较好的结果，因此目前依然是工程问题中模拟湍流的基本方法。

3. 常见湍流模型及其适用性

1）Spalart-Allmaras（SA）模型

SA 模型是一个单方程模型，该模型求解湍流运动黏性ν~的输运方程。SA 模型是专门为航空航天工程问题设计的湍流模型，在壁面边界层流动、逆压梯度流动等问题上表现优秀，并且广泛用于涡轮机械领域。

SA 模型中求解湍流运动黏性ν~的输运方程为(www.daowen.com)

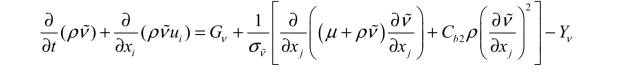
其中，ρ 为流体密度； ui 为流体速度分量；Gν 为湍流黏性生成项；Yν 为湍流黏性耗散项；νσ ~与Cb2 为模型常数。

需要注意的是，除航空航天工程中的气动问题外，SA 模型并不具有普适性。对于自由剪切流与射流问题，SA 模型会引入较大的误差。

2）realizable k−ε （RKE）模型

RKE 模型是一个两方程湍流模型，该模型求解湍流动能k 与湍流耗散率ε 的输运方程，再通过k 与ε 计算得到湍流黏性 tμ 代入雷诺平均NS 方程中。其求解的输运方程为

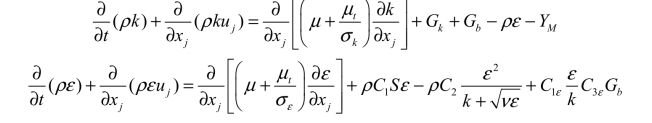
其中

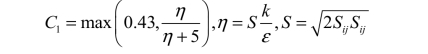
其中，μ 为分子黏性； kσ 与 εσ 分别为湍流动能与湍流耗散率普朗特数； C2 与 1C ε 为常数。

求解输运方程后，根据下式计算湍流黏度 tμ 。

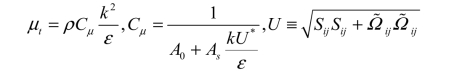
引入应变率张量对湍流黏性的影响后，RKE 模型显著改善了k−ε 模型对于圆管射流模拟的可靠性，并提高了大曲率旋转流动与大应变流动的模型精度。需要注意的是，由于RKE模型本身只适用于充分发展的湍流流动，因此在近壁面区域必须结合壁面函数（wall functions）以确保近壁面流动的合理性。

3）shear stress transport（SST）模型

虽然RKE 模型对于射流流动能够给出较为合理的结果，但是在实际工程问题中，射流流动经常与壁面冲击结合在一起。近壁面流动对射流冲击区域的流动参数影响较大，而RKE 模型本身并不能解析边界层流动的细节。SST 模型克服了RKE 模型的缺陷，能够较好地解析边界层流动。该模型同样是两方程模型，与RKE 模型的区别在于，SST 模型是基于k−ω 模型的，其中，ω 为比湍流耗散率，即湍流耗散率与湍流动能之比。其输运方程为

其中，Γk 与Γω 分别为湍流动能与比湍流耗散率的有效扩散率。

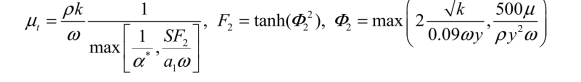
y 为网格单元中心点到壁面的距离。

SST 模型能够较好地模拟逆压梯度流动、近壁面流动分离，因此适用于研究射流冲击区域的流动特性。值得注意的是，SST 模型需要额外求解网格单元到壁面的距离，因此其计算效率要低于RKE 模型。