本章前面的内容都是针对一维流动展开讨论，下面拓展到多维流动。三维欧拉方程的守恒律形式微分方程为

其中

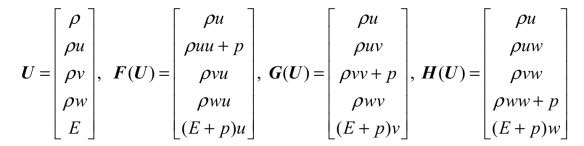
总能量为

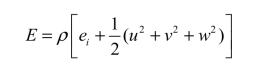
式（4.66）的积分形式为

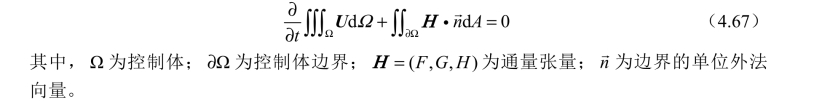
1. 旋转不变性

边界的单位外法向量可以表示为［1］

其中， 1θ 和 2θ 为直角坐标系下，单位外法向量的两个方向角。于是三维欧拉方程满足如下关系式：

其中

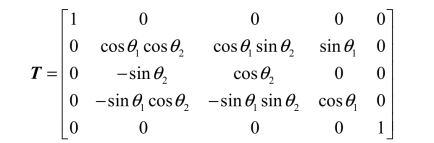
2. 方向分裂欧拉方程

采用数值的方法求解多维欧拉方程时，常常要用到方向分裂的欧拉方程，以x 方向为例，x 向分裂欧拉方程的守恒律形式为

其中

x 向分裂欧拉方程的黎曼问题为

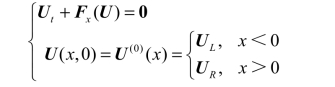
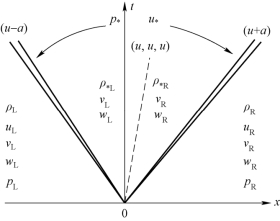
其解的结构如图4.27 所示，中间的三道波对应同一个接触间断，跨过这个间断时ρ、v 、 w发生跳跃，而u、 p 保持不变。

(www.daowen.com)

图4.27　x 向分裂欧拉方程的黎曼解

星域的左半部分的切向速度为

右半部分切向速度为

其余黎曼解与一维欧拉方程的黎曼解保持一致。因此，一维欧拉方程的黎曼求解器可直接用于求解x 向分裂欧拉方程的黎曼问题。

3. 结构化网格求解多维欧拉方程

由四边形网格（二维问题）或六面体网格（三维问题）构成的拓扑结构单一的网格称为结构化网格。对于中心存储的有限体积法而言，一般的二维结构化网格示意如图4.28 所示。

在实际使用的过程中，常用到规整的二维结构化网格，如图4.29 所示。

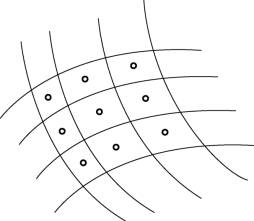
图4.28　一般的二维结构化网格示意

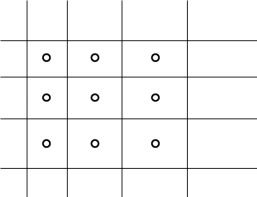
图4.29　规整的二维结构化网格示意

结构化网格求解三维欧拉方程，可以采用方向分裂的方法，将式（4.66）分裂成3 个与式（4.68）结构类似的方程组，即

再根据空间重构的精度选择匹配的时间离散格式，更新单元均值。

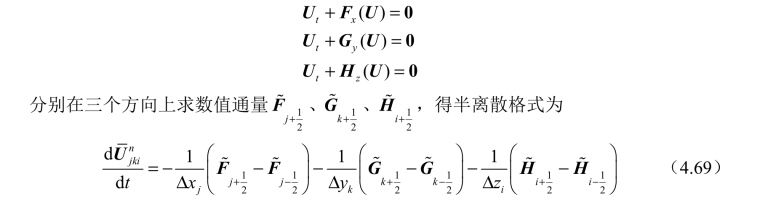
4. 非结构化网格求解多维欧拉方程

结构化网格以外的网格为非结构化网格，在二维问题中可包含任意多边形，三维问题中可包含任意多面体。典型的二维非结构化网格如图4.30 所示。

在非结构化网格上采用有限体积法求解三维欧拉方程，需要应用其积分形式，即式（4.67）。应用单元均值的定义，可将其写成

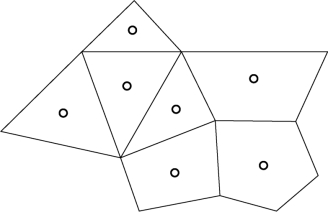
图4.30　典型的二维非结构化网格