3.1 节建立了绝热无黏准一维喷管流动的定常控制方程，这里重新建立微分形式的非定常控制方程。准一维拉瓦尔喷管及控制体模型如图4.25 所示。

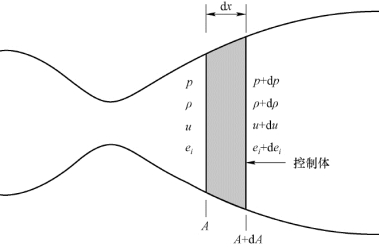
图4.25　准一维拉瓦尔喷管及控制体模型

1. 质量方程

从积分形式的式（2.9）开始，即

其中

式（4.57）的第二项为流出控制体的总质量

将上式展开并略去二阶及以上高阶项，可得

于是可得质量方程为

方程两端同时除以dx，并利用 ∂A /∂t= 0，进一步可得

注意观察式（4.58），是在欧拉方程的质量方程上增加了一个与面积相关的源项。

2. 动量方程

积分形式的动量方程为

其中

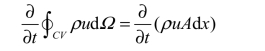
流出控制体的总动量为

式（4.59）右端项为控制体表面所受压力在x 方向的分量，如图4.26 所示。

(www.daowen.com)

图4.26　控制体表面所受压力

将上述三项代入式（4.59）可得

同质量方程，方程两端同时除以dx，并利用 ∂A /∂t= 0可得

式（4.60）是欧拉方程的动量方程加上右端的源项。

3. 能量方程

控制体的能量守恒可以表述为

其中

流出控制体的总能量为

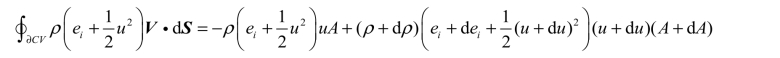
略去高次项可得

对于压强做功的项，注意壁面上的压强不做功，因此：

略去高次项有

上述项代入式（4.61）可得

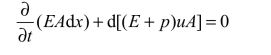
进一步有

式（4.58）、式（4.60）和式（4.62）构成了绝热无黏准一维非定常流动的控制方程组，分别是欧拉方程的各个方程加上一个源项的形式。因此，只需对源项进行适当处理，欧拉方程的数值解法便可直接推广至该方程组。