Godunov 型有限体积法求解欧拉方程的基本步骤与求解双曲方程组基本一致。考虑欧拉方程的守恒律形式（4.41），网格和第n 个时间步的单元均值如图4.23 所示。

图4.23　网格和第n 个时间步的单元均值

对于欧拉方程，同样有类似于式（4.16）的半离散格式，即

为了更新单元内的均值，需要求得面上的数值通量。数值通量的求解通常采用黎曼求解器，为此需要知道每个面左右两侧的状态。从第n 个时间步的单元均值得到面的左右状态，需要进行重构。因此，求解欧拉方程的步骤分为重构、求解数值通量和更新单元均值。

1. 重构

重构时根据重构的变量不同可分为守恒变量重构、原始变量重构和特征变量重构。

1）守恒变量重构

重构变量为

由于每个时间步更新的值即是守恒变量，重构之前不需要做任何变换。

2）原始变量重构

重构变量为(www.daowen.com)

这种重构方式，需要在重构之前将上个时间步更新的守恒变量转换为原始变量，转换的依据是状态方程。

3）特征变量重构

重构变量为

这种重构方式，需要先根据状态方程将守恒变量转换为原始变量，再求得每个单元内的特征变量的均值。

2. 求解数值通量

以任一方式完成重构之后，得到每个面左右两侧的状态。以守恒变量重构为例，如图4.24所示。

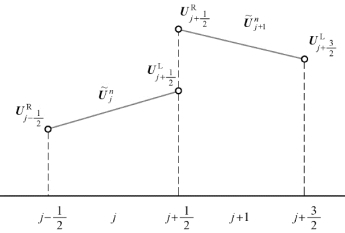
图4.24　守恒变量重构示意

此时便可利用黎曼求解器求解每个面上的数值通量，如HLL 或HLLC 黎曼求解器。在根据式（4.53）或式（4.54）求解数值通量之前，可能需要利用状态方程和特征变量与原始变量的关系完成重构变量至所需变量的转换。

3. 更新单元均值

利用黎曼求解器求得面上的数值通量之后，再根据4.2.4 小节的高阶时间格式更新守恒变量的单元均值，需要注意的是时间格式的精度要与空间重构格式的精度匹配。具体来说，一阶空间重构可直接应用后向差分时间推进，TVD 格式则需二阶时间格式，三阶及以上的（W）ENO 格式需要应用三阶及以上的时间格式。