对于一维欧拉方程的守恒律形式，其黎曼问题可表述如下［1］：

欧拉方程黎曼问题解的结构如图4.19 所示。

图4.19　欧拉方程黎曼问题解的结构

3 个特征速度对应的3 个波将x−t平面分成4 个区域，从左至右依次为U L、U *L、U *R 和U R。中间的 U *L和 U *R区域合称为星域（star region）。特征值 λ 2 = u对应的波为接触间断，跨过接触间断时速度和压强保持不变，而密度等其余量发生变化。特征值 λ1 ,3 = u ± a 则对应稀疏波或者激波，跨过稀疏波和激波时密度、压强和速度都将发生变化。

需要注意的是，欧拉方程是非线性方程组。因此一般情况下，这里的3 个波的波速并不等于各自对应的特征速度。关于欧拉方程黎曼解的非线性波的特性分析和据此求得的黎曼问题精确解请参考下面的扩展阅读。

扩展阅读

TORO E F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction［M］．Berlin：Springer，2009.

第3 章、第4 章

求欧拉方程黎曼问题的精确解需迭代的过程，计算量较大。在实际应用Godunov 型方法时，通常采用近似黎曼求解器（approximate Riemann solver，以下简称“黎曼求解器”），下面简要介绍两种。

1. HLL 黎曼求解器

考虑黎曼问题（4.43），其精确解被包含在控制体[ xL , xR ] ×[0, T]内，如图4.20 所示。

图4.20　包含黎曼问题控制体

这里 SL 和 SR 是最快的波速，区间长度满足：

在控制体内对守恒律（4.43）积分可得

从而有

即

综合式（4.45）和式（4.46）可得

将式（4.48）代入式（4.50）或式（4.51）可得

所谓的HLL（Harten，Lax，van Leer）黎曼求解器，是假定图4.19 的星域内是常值区域，其状态为U hll ，过t 轴的通量由F hll近似，即忽略了第二道波的影响，只求平均状态。HLL黎曼求解器解的结构如图4.21 所示。

图4.21　HLL 黎曼求解器解的结构

HLL 黎曼求解器由Harten、Lax 和van Leer 提出，其解为

t 轴的数值通量为

HLL 黎曼求解器具有良好的稳定性，即使求解较强的正激波也不会产生明显振荡。但其缺点在于无法较好地处理接触间断、剪切波和相间界面等包含第二道波的问题。为此Toro、Spruce 和Speares 在HLL 求解器的基础上提出了HLLC 求解器，C 代表的是contact，即该求解器将中间的波也考虑进去，构成了完备的黎曼解。

2. HLLC 黎曼求解器

HLLC 黎曼求解器解的结构如图4.22 所示。

图4.22　HLLC 黎曼求解器解的结构

第二道波的波速为 *S ，这里不加证明地给出：

(www.daowen.com)

这道波将星域分割成 U*L 和U*R 两个常值区域为

其中，K =L 或R，且

数值通量为

由于跨过接触间断时压强和速度保持不变，星域的压强应该是常值，因此HLLC 求解器可以有另一种形式的解。星域的压强为

星域的状态向量为

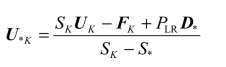
星域的数值通量可表示为

求得星域的解之后，HLLC 求解器的解为

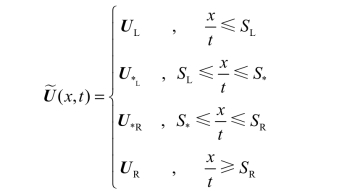
t 轴的数值通量为

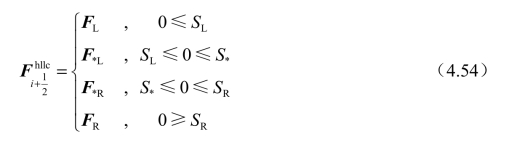
3. 速度估计

为了利用HLL 或HLLC 黎曼求解器求解面上的数值通量，需要估计波的最快传播速度S L和 S R。这一估计对计算的稳定性有较大影响，因为在应用Godunov 型方法求解欧拉方程时，与对流方程稳定性条件（4.33）类似，也需要满足稳定性条件：

其中

在HLL 和HLLC 求解器的发展史上，提出了多种速度估计方法，其中两种常用的直接估计方法如下。

1）Davis 简单估计

直接应用特征速度估计最快波速：

或者

2）Roe 估计

利用Roe 平均估计最快速度：

或者

其中

h 为比焓：

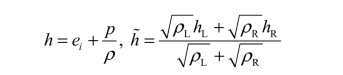
关于HLL 和HLLC 黎曼求解器的详细介绍以及其他常用黎曼求解器，请参考下面的扩展阅读。

扩展阅读

TORO E F. Riemann solvers and numerical methods for fluid dynamics: a practical introduction［M］．Berlin：Springer，2009.

第8 章至第12 章