Godunov 方法提供了一种求解偏微分方程的思路，即在单元边界上构造局部黎曼问题，求解黎曼问题得（数值）通量，再根据守恒律更新单元的平均值。但由于其在时间和空间上均只有一阶精度，格式的数值耗散较大，往往不能满足实际应用的需求，如4.2.3 小节的测试算例。

为了减小格式的数值耗散、提高解的精度，需要同时提升空间离散和时间离散的精度。

1. 高阶重构格式

Godunov 方法在空间上只有一阶精度是由于其“单元内部物理量均匀分布”的假设，为了提高空间离散精度，可采用更高阶次的多项式近似。根据单元均值去估计单元内部物理量的分布的过程称为重构。假定重构所得单元内部值的分布为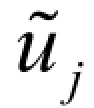 ( x)，重构的约束条件是

Godunov 方法的重构采用0 次多项式，称为分片均匀（piecewise constant）重构。还可以采用一次、二次甚至更高次的多项式重构，并由此派生出一系列Godunov 型方法。下面以一次多项式为例展开讨论。

依然考虑对流速度a＞0 的对流方程（4.10），网格及单元内部物理量的分布如图4.12 所示。为便于讨论，此处采用宽度为 Δx 的均匀网格。

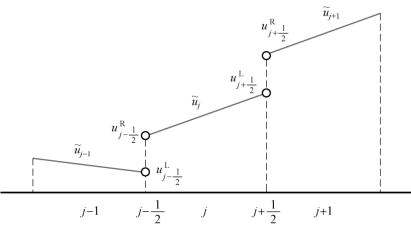
图4.12　网格及单元内部物理量的分布

据此可求得

从而求得面上的重构值：

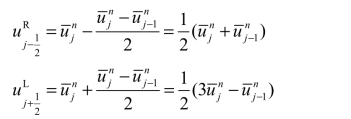
由式（4.30）和式（4.31）可得

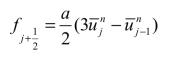
同理可得

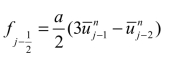
将通量表达式代入式（4.16），可得如下离散格式：

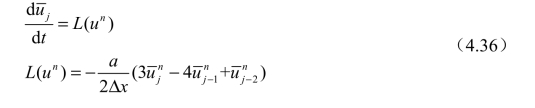
2. 高阶时间格式

采用高阶重构时，图4.12 所示的一次多项式重构，每个面两侧的状态不再构成经典的局部黎曼问题。但在求解数值通量时，Godunov 型方法仍然采用经典黎曼问题的解。为了减小这一近似带来的不匹配问题，需要采用高阶时间推进方法，典型的如高阶Runge-Kutta 法。这里简单介绍一类强稳定性Runge-Kutta 法，详细介绍请参考下面的扩展阅读。

扩展阅读

GOTTLIEB S. On high order strong stability preserving Runge-Kutta and multi step time discretizations［J］．Journal of scientific computing，2015，25（1−2）：105−128.

4.5 节

对于常微分方程：

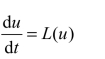
1）两段二阶强稳定性Runge-Kutta 法

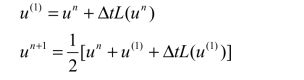
2）三段三阶强稳定性Runge-Kutta 法

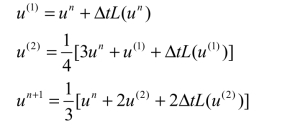
3）五段四阶强稳定性Runge-Kutta 法

3. TVD 格式

结合式（4.36）和两段二阶Runge-Kutta 法，可得时间和空间精度均为二阶的线性离散格式。

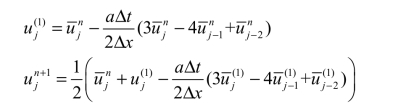
采用4.2.3 小节的数值测试算例测试上述格式。图4.13 为二阶线性格式 t=0.05时刻的数值解，可见解在多个局部产生了振荡，这说明上述格式是不稳定的。

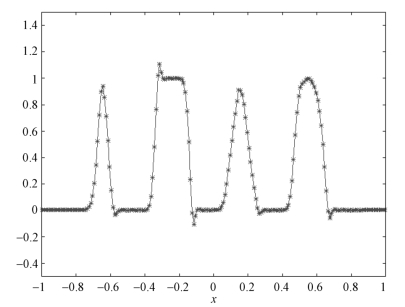
图4.13　二阶线性格式t = 0.05 时刻的数值解

1）Godunov 定理

一个用于求解偏微分方程的线性数值格式，如果它能不产生新的极值（单调格式），则它最多只能有一阶精度。

所谓线性数值格式，是指形如(www.daowen.com)

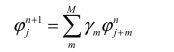
的格式，其中的系数 mγ 与离散点值无关。显然，上述二阶格式为线性格式。根据Godunov 定理，它必然是不稳定的。

Godunov 定理在CFD 领域占有极其重要的地位，它事实上指出了构造稳定的高阶格式的途径——引入非线性系数。TVD（total variation diminishing，总变差递减）格式正是基于这一思想，引入了非线性的梯度限制器。

TVD 格式在式（4.35）的基础上引入梯度限制器ψ ( r) ：

其中

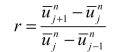
2）总变差递减

考虑图4.14 所示的离散数据［5］。

其总变差定义为

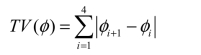
总变差递减是指对于任意时间步n：

1983 年Harten 证明，保单调的格式必然满足TVD 条件，反之亦然。

1984 年Sweby 给出了数值格式具备TVD 性质的充要条件，即

在r−ψ( r)平面上，TVD 条件如图4.15 中的阴影区域所示。

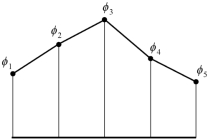
图4.14　离散数据

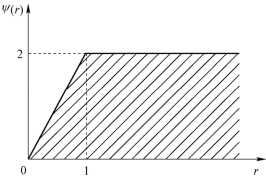
图4.15　TVD 条件

1984 年，Sweby 给出了二阶精度TVD 格式的条件，即

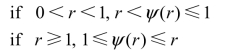
在r−ψ( r)平面上，二阶精度TVD 条件如图4.16 中的深色区域所示。

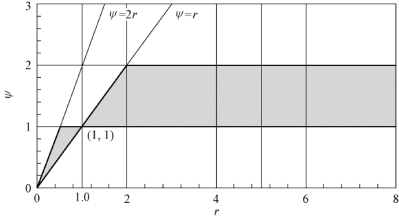
图4.16　二阶精度TVD 条件

在这些条件下，发展了一系列二阶精度TVD 格式，如表4.1 所示。各个TVD 格式的精度大致相当，但计算量存在差异。格式的选择更多地依赖于实际问题和经验，没有一致精确的理论分析表明某种格式优于其余格式。图4.17 和图4.18 分别给出了采用4.2.3 小节的数值算例测试min-mod 限制器和van Leer 限制器的结果。虽然min-mod 格式的结果耗散较大，但与图4.11 Godunov 方法的结果相比，两者都有明显的改善。

表4.1　二阶精度TVD 格式

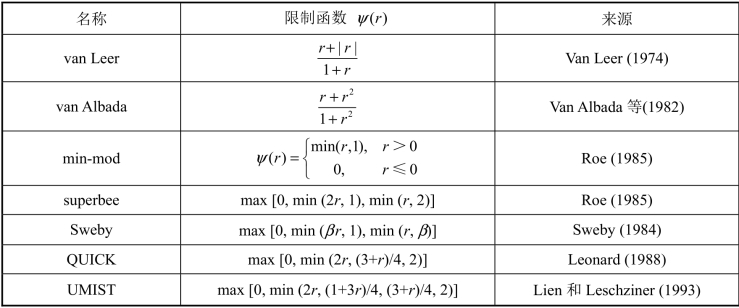
图4.17　min−mod 限制器t = 2.0 时刻的数值结果

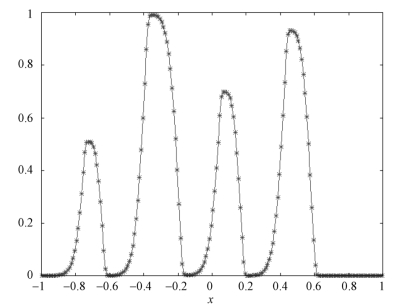
图4.18　van Leer 限制器t = 2.0 时刻的数值结果

扩展阅读

VERSTEEG H K，MALALA-SEKERA W. An introduction to computational fluid dynamics：the finite volume method［M］．2nd ed. Glasgow: Pearson Education Limited，2007.

5.10 节

4.5 节

4. ENO 和WENO 格式

TVD 格式可以达到二阶精度，要想得到更高阶精度的格式，需要采用ENO（本质无振荡）或WENO（加权本质无振荡）思想，利用更高次的多项式重构。详细的方法介绍请参考下面的文章。

扩展阅读

ZHANG Y T，SHU C W. ENO and WENO schemes［J］．Handbook of numerical analysis，2016（17）：103−122.