有限体积法的基本思想在4.1.2 小节做了简要介绍，下面来讨论一种适合于求解可压缩流的有限体积法——Godunov 方法。该方法于20 世纪60 年代由Godunov 提出，开创了有限体积法的一大分支。

考虑对流速度a＞0 的对流方程（4.10），有限体积法的网格定义与第n 个时间的步单元均值分布如图4.7 所示。

对于任何有限体积法来说，式（4.16）严格成立，即

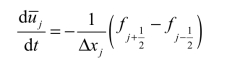
因此，构造离散点值的代数表达式需要两步。

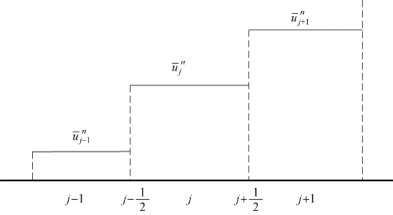
图4.7　有限体积法的网格定义与第n 个时间的步单元均值分布

1. 数值通量

Godunov 方法的基本思想是，假定物理量在单元内均匀分布，在单元的每个面上构造一个局部黎曼问题，通过求解黎曼问题来求得面上通量。

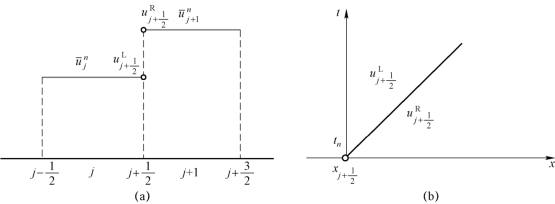
图4.8　局部黎曼问题及其解

（a）局部黎曼问题；（b）局部黎曼问题的解

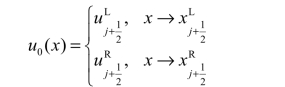
假定物理量在单元内均匀分布，有

由于a＞0 ，做出该局部黎曼问题的解的结构，如图4.8（b）所示。因此，该局部黎曼问题的解为

代入式（4.30）可得

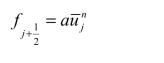
同理可得

2. 时间离散

式（4.16）中时间导数项也需要由离散点值来表达，Godunov 方法直接用有限差分来近似，即

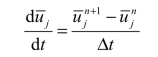(www.daowen.com)

将通量和时间差分代入式（4.16）可得Godunov 方法的完整离散格式：

3. 稳定性条件

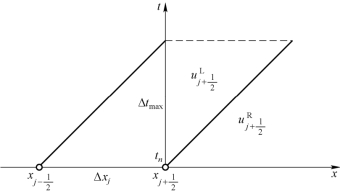
图4.9　稳定性条件

稳定性分析也可以采用冯·诺依曼方法，请参考如下扩展阅读。

扩展阅读

ANDERSON J D. Computational fluid dynamics: the basics with applications［M］．New York: McGraw-Hill，Inc.，1995.

4.5 节

4. 数值精度

下面来考察离散格式（4.32）与对流方程（4.7）之间的差异。

借用有限差分法的分析方法，有如下泰勒展开式：

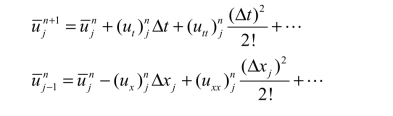
算术运算可得

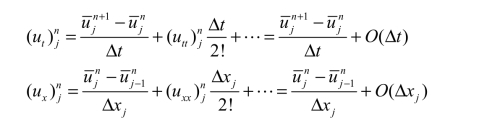
代入对流方程可得

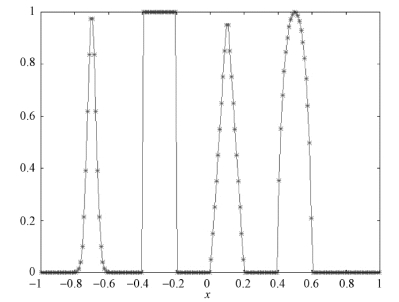
图4.10　初始条件

左右两端采用周期性边界条件，精确解为初始形状以对流速度向右循环移动，保持形状不变。图4.11 为采用Godunov 方法得到的一个周期之后的数值解，可见各个峰值都被严重抹平。

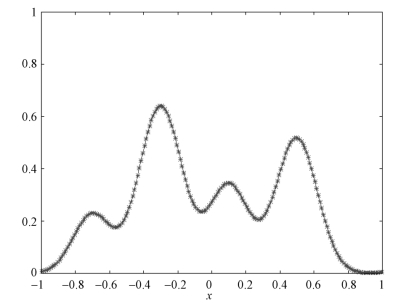
图4.11　t = 2.0 时刻的数值解