下面将对流方程的分析扩展至包含m 个方程的双曲方程组［1］。

由于A 的所有元素均为常数，矩阵K 的所有元素均为常数，利用式（4.23）和式（4.24）可将原方程组改写为

进一步在方程组上左乘−1K 可得

展开成标量形式即为

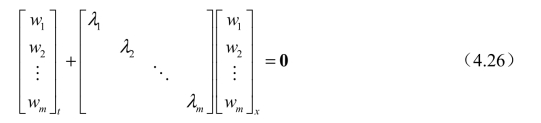
或记为

通过这一线性变换，原方程化为等价的m 个完全解耦的对流方程，特征速度即矩阵A 的特征值。变量W 称为原变量U 的特征变量，方程（4.25）称为原方程的特征方程。

考虑方程组（4.26）的初值问题，其初始条件为

根据式（4.24）可将该初始条件转为特征方程的初始条件：(www.daowen.com)

再由4.2.1 小节得到的对流方程的理论解，可直接求得特征方程的解：

进一步有原方程的解：

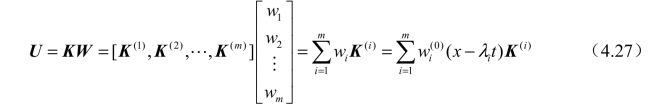
考虑严格双曲方程组的如下初值问题［1］：

注意到式（4.29）是式（4.27）在 t=0 时的特殊情况，因此有特征方程的初始条件为

从而可得

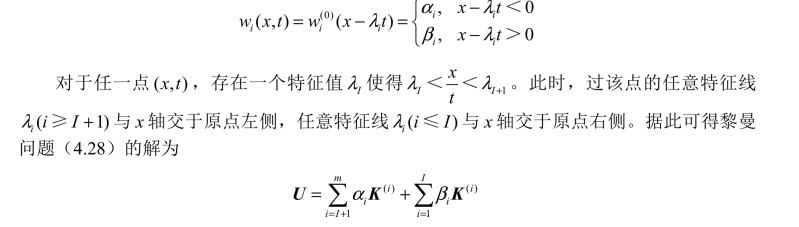
该解具有图4.6 所示的结构，m 条特征线将x−t 平面分割为m+1 个常值区域。每跨过一条特征线，解就经历一次跳跃。传播速度为 1λ 的特征线左侧区域的解为UL ，传播速度为 mλ 的特征线右侧区域的解为UR 。

图4.6　线性双曲方程组的黎曼解