考虑如下初值问题［1］：

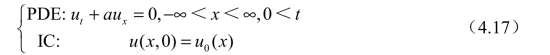
对于形如对流方程的偏微分方程，其特征线定义为沿x−t 平面的某一条线x =x ( t)，偏微分方程可以写成全微分方程。

沿线x =x ( t)有

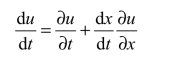
如果满足常微分方程：

则有

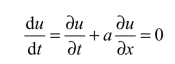
也即沿线x =x ( t)函数值 u ( x , t) 保持不变。因此，满足方程（4.18）的线为对流方程的特征线，它们是一系列平行直线，构成对流方程的特征线族，如图4.3 所示。沿着每一条特征线函数值保持不变，参数a 也被称为特征速度。

根据上述特征线的特性，可直接得到初值问题（4.17）的理论解。

这个解的物理含义是，给定初始条件，对流方程将初始条件以速度a 向右(a＞0) 或向左(a ＜0) 平移，并保持解的形状与初始条件一致。

下面来看一类特殊的初值问题［1］：(www.daowen.com)

图4.3　对流方程的特征线

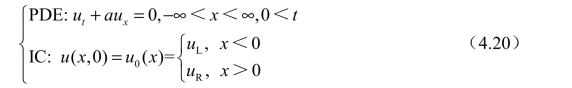
初始条件是以x=0 为界，左右两侧均为常值，如图4.4 所示。

根据式（4.19）可以直接得到该黎曼问题的理论解为

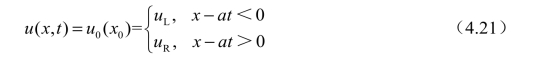
该解的含义是，在x−t平面上的直线x−at= 0将平面分为左右两个区域，左侧所有点的解都为u = uL ，右侧为u = uR ，如图4.5 所示。

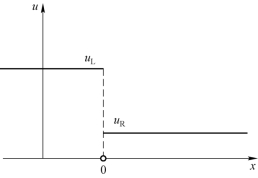
图4.4　黎曼问题的初始条件

图4.5　对流方程黎曼问题的解

直线x−at= 0正是双曲方程在 x0 = 0处的特征线，即对流方程黎曼问题的解是初始间断点处的特征线将解平面分割而成的两个常值区域，在射线 x /t= 0上的解为u (0, t )= uL。

如果此处对流速度a ＜ 0，则黎曼问题的解与图4.5 相反，特征线位于第二象限，在射线x /t= 0上的解为u (0, t )= uR 。

综合上述分析，射线 x /t= 0上的解总是位于其上游的状态，即迎风方向的状态。求解黎曼问题的过程实际上是寻找迎风解的过程，而对流问题的求解必须考虑迎风特性，即流动方向对解的依赖性的影响。在纯粹的对流问题中，如这里的对流方程，解只依赖于其上游的状态，即迎风方向的状态，而与下游的状态无关。求解对流问题的数值方法，若不考虑这种迎风特性，将是不稳定的。