当前求解偏微分方程的数值解的方法主要有有限差分法（finite difference method，FDM）、有限元法（finite element method，FEM）、谱方法（spectral method）和有限体积法（finite volume method，FVM），以及由这些方法派生出来的一些混合型方法。下面以对流方程为例，简单阐述各个方法的基本思想。

1. 有限差分法

FDM 的基本思想［4］是，关注定义域内一系列离散点处的解，以有限差分近似微分方程中的导数项，得到离散点的近似值的代数关系，进而演化出方程的数值解。有限差分法的离散点如图4.1 所示。

如图4.1 所示，FDM 关注的是离散点( x j , t n )。其中j=1,2,… ,j为空间网格点的编号，n=0,1,… ,n代表时间步，n= 0为初始时刻。考虑对流方程（4.7）：

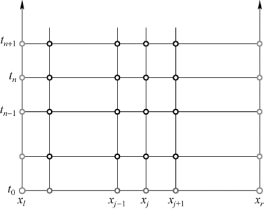
图4.1　有限差分法的离散点

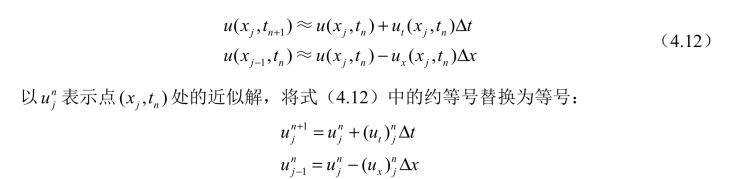
由此可得导数项的有限差分近似：

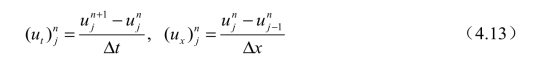
将式（4.13）代入对流方程，得到近似的代数方程，称为差分方程：

给定初始条件（t = t0时刻各网格点的值）和边界条件（此处只需x = xl 处各时间步的值），即可根据式（4.14）求得其他所有离散点的值。

2. 有限体积法

FVM［1］的基本思想是，关注定义域内的一系列离散单元的积分平均值，采用近似的方法求得单元各面上的通量，再利用微分方程的积分形式求得积分均值的演化。有限体积法的离散单元如图4.2 所示。

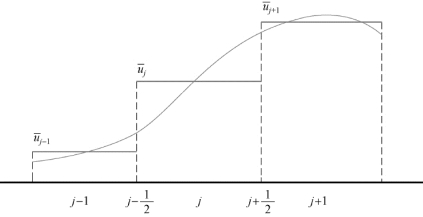
图4.2　有限体积法的离散单元

考虑对流方程（4.10），对流速度a＞0 。定义网格内的单元均值为(www.daowen.com)

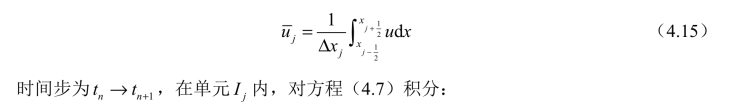
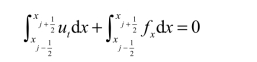
对于积分所得第一项，有

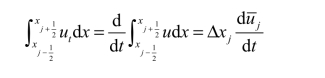
积分所得第二项，有

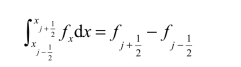
将上述代入对流方程（4.10）可得半离散格式

式（4.16）中的时间导数项，可采用有限差分近似：

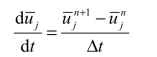
将数值通量和时间项的有限差分代入式（4.16）可得

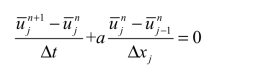
3. 混合型方法

上述两种偏微分方程的数值解法各有其优缺点。

有限差分法可以基于泰勒展开式，思路明晰，很容易推广至高精度格式。但它直接利用方程的微分形式，在遇到激波和界面等间断时易发生数值振荡。

有限体积法基于方程的积分形式，具有良好的守恒性质，适合于处理可压缩流的问题。

一些混合型方法将上述两种方法结合起来，取长补短。

燃气射流是典型的可压缩流动，包含复杂的激波结构，有时还会涉及相间界面问题，因此采用有限体积法或其他方法与有限体积法的混合方法是最合适的。本章后续内容将介绍有限体积法中的一类方法，即Godunov 型方法。