根据人们日常的直观感受，如果流场的各个边界条件保持不变，那么流场内部应该逐渐趋于一个稳定的状态。事实上，许多情况下这种直觉是正确的。然而，在涉及燃气射流的工程问题中，即使工况条件不随时间变化，得到的燃气射流依然表现出明显的不稳定性。这种不稳定性集中体现在燃气射流混合边界层区域，也是造成发射时结构振动与“轰鸣声”的罪魁祸首。那么，燃气射流的流动不稳定性究竟是如何产生的呢？如图3.16 所示。

图3.16　燃气射流流动不稳定性

图中不同颜色表示不同的燃气质量分数（见彩插）

1. 瑞利−泰勒不稳定性

瑞利−泰勒不稳定性（Rayleigh-Taylor instability）简称为RTI，指的是在重力作用下，微小扰动使得位于上方的密度较大的流体向下方密度较小的流体流动，进而导致两种流体交界面失去稳定的现象。图3.17 为典型的水−油系统RTI 现象。位于上方的密度更大的水受到微小扰动，在重力作用下向下运动，下方的油受到挤压向上运动。这种在重力作用下由于微小扰动产生的两种流体之间的相互运动破坏了水−油水平交界面在竖直方向的稳定性。同时，RTI 增强了水和油之间的对流，促进了水和油的相互混合（这里的混合并不意味着溶解）。

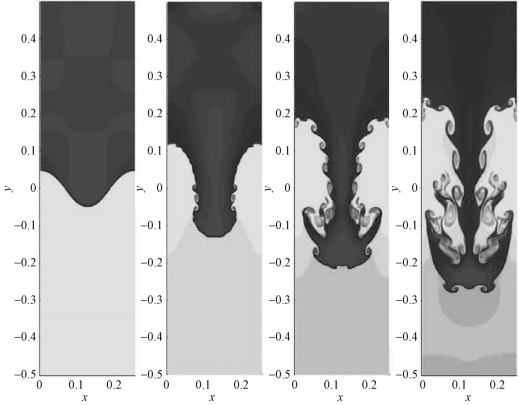
图3.17　典型的水−油系统RTI 现象^[1]

为了进一步解释RTI 现象的本质，我们可以将图3.17 中的水和油抽象成通过连杆相连的两个具有不同质量的小球。如图3.18 所示，两个小球的质量m2＞ m1，上方质量较大的小球代表密度较大的流体，下方质量较小的小球代表密度较小的流体，连接两个小球的连杆中央位置通过铰接固定，初始时刻连杆处于竖直方向。显然，虽然此时系统达到了平衡状态，但是这种平衡是不稳定的，一个极其微小的扰动就会使得系统在重力作用下发生反转，且无法自发回到原来的平衡状态。也就是说，在这种非稳定平衡状态下，一旦受到微小扰动影响，系统的势能就会自发转化为动能，这也是产生RTI 现象的根本原因。

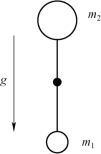
图3.18　不稳定系统简化模型(www.daowen.com)

对于燃气射流而言，RTI 现象是极为常见的。例如，在大气层中飞行的导弹所产生的燃气射流，其与周围空气之间存在密度差，因此在混合边界层中必然存在RTI 现象。我们平时观察到的导弹尾焰边界层随时间不断波动变化的过程就蕴含着RTI 现象。

2. 开尔文−亥姆霍兹不稳定性

开尔文−亥姆霍兹不稳定性（Kelvin-Helmholtz instability）简称为KHI，于1868 年由亥姆霍兹首先发现，并于1871 年由开尔文进行了定量分析。其普遍存在于两种流体的剪切交界面处。两种流体既可以是同一相（如同是气体或同是液体），也可以是两相（气−液交界）。前者难以观察到明确的交界面，两种流体之间的剪切体现为具有一定厚度的混合边界层；后者则具有明确的、可以观察的相间交界面。燃气射流中的KHI 属于前者，其中剪切作用产生于燃气射流与周围空气之间的速度差。

KHI 现象的产生机理在于速度差导致两种流体之间产生剪切，进而形成涡，如图3.19 所示。涡的存在使得两种流体之间进行物质、动量和能量交换，同时也使得二者之间的交界面变得逐渐“模糊”。当二者速度差较小时，这些涡始终保持在一定尺度范围内，达到动态平衡状态；而当速度差足够大时，涡的尺度将持续增大，使得系统逐渐转为非平衡状态，在边界层区域显示出不稳定性。例如，图3.19 中RT 失稳后的流体交界面有一部分从水平方向变为竖直，由于两种流体在竖直方向存在剪切，因此在剪切区域生成涡旋，进而导致竖直方向交界面在水平方向发生KHI 现象。同时，KHI 现象中的涡意味着KHI 与湍流的密切联系，尤其是从层流到湍流的转捩。

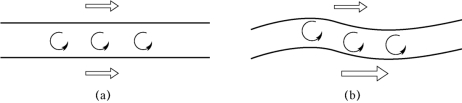
图3.19　KHI

（a）稳定剪切状态；（b）不稳定剪切状态

对于在交界面两侧物理量连续的两种流体，人们通常使用理查德森数Ri 判断是否会出现KHI 现象。Ri 在物理上表示浮力与剪切力之比，定义为

其中，g 为重力加速度；ρ 为交界面处流体密度；u 为流体流动速度；z 为垂直于交界面方向的坐标分量。当Ri ＞0.25时，系统必然是KH 稳定的，只有当Ri ＜0.25时才会出现KHI现象。显然，在无重力/等密度条件下，Ri =0 ，此时系统是RT 稳定的，但依然可能是KH不稳定的。可见，虽然KHI 有时伴随着RTI 出现，但是KHI 并不要求重力与密度差的存在，这说明二者并没有本质关联。