不同于正激波，斜激波与来流之间的夹角β ＜ 90°。产生斜激波的典型情形为超声速来流流过楔形体后发生偏转，如图3.14 所示。相比于正激波，斜激波受到阻挡后的流动偏转角θ 较小。根据质量守恒，可以得到

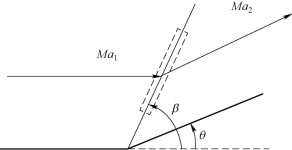
图3.14　斜激波

其中， u1n 与 u2n 为波前与波后法向（垂直于斜激波）速度分量。由切向（平行于斜激波）动量守恒可知

其中， u1t 与 u2t 为波前与波后切向速度分量。将式（3.138）与式（3.139）联立后可得

可见，激波前后切向流动速度不变，只有法向速度分量发生突变。因此，我们可以把斜激波看作是相对于法向速度分量的正激波。这样，我们可以通过把马赫数M1a 代换成法向马赫数Ma1 ·sinβ，直接将正激波的流动关系式改写为斜激波流动关系。

1. 压强比 p 2/p1

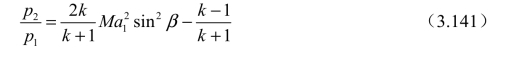
2. 速度比u2 n/u1n

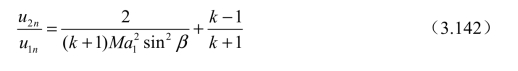
3. 密度比 ρ 2/ρ1

4. 温度比 T2 /T1

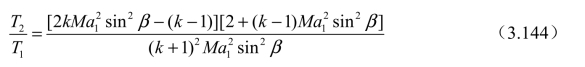
5. 波后马赫数Ma2

首先，定义法向马赫数为(www.daowen.com)

将Ma1n 和Ma2n 分别代入正激波马赫数关系式（3.121）中的Ma1 和Ma2 可得

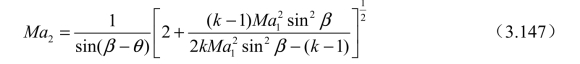
式（3.147）中既包含激波角β ，又包含流动偏转角θ 。实际上，考虑到激波前后总温不变，可以得到

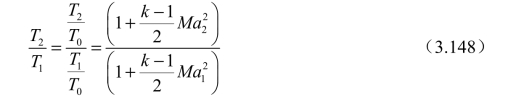
代入温度比关系式（3.144）可得

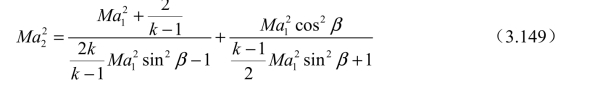
6. 总压比p0 2/p01

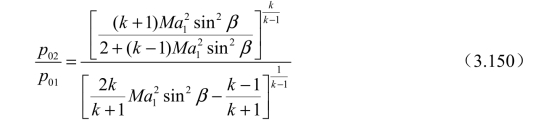
7. 激波角β 与偏转角θ 的关系

如前所述，在斜激波关系式中，激波角β 是普遍存在的。然而，目前为止，我们还不清楚激波角β 的表达式。从激波形成的机理来看，激波角β 取决于偏转角θ 以及来流马赫数Ma1 。将式（3.140）与式（3.142）联立，并考虑到

可以得出

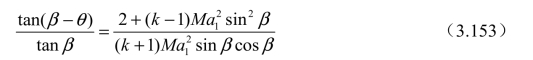
8. 朗金−雨贡纽关系式

将式（3.141）与式（3.143）联立后消去Ma1 sinβ 可得

显然，斜激波的朗金−雨贡纽关系式与正激波是一致的。也就是说，朗金−雨贡纽关系式对于激波前后流动参数比值关系具有普适性，与具体的偏转角大小无关。