多个弱压缩波汇聚在一起形成的强压缩波称为激波。当超声速气流受到壁面阻挡产生有限角度的偏转时就会产生激波。气流越过激波后，密度、速度、压强、温度等流动参数会产生阶跃，而激波本身的厚度仅为分子平均自由程的数倍。因此，气流流过激波的过程是典型热力学的非平衡态过程，所以必然是非等熵的。激波的存在是超声速气流的典型特征，也是燃气射流中的典型流动现象。例如，飞机与火箭尾焰中的马赫环就是由激波反射形成的。

考虑到激波前后流动参数的显著变化以及激波本身极小的厚度，我们在数学上一般将激波视为一个没有厚度的间断面。根据激波与超声速来流之间的夹角（激波角），又有正激波与斜激波之分。正激波的激波角β =90 °，斜激波的激波角β ＜90 °。一般而言，正激波要强于斜激波，即正激波波前与波后流动参数的差异更为明显。

我们先分析正激波波前与波后流动参数之间的关系。如图3.13 所示，超声速来流垂直冲击平板，由于平板的阻挡，在平板前会形成一道正激波。这一过程也可以看作是将图3.12（b）中的偏转角θ 增大到90°。由于一般情况下，波前参数是已知的，因此实际上我们需要用波前参数得到波后参数。取图3.13 所示的控制体，同时假设流动是无黏、绝热的，气体为理想气体，根据质量守恒定律，有

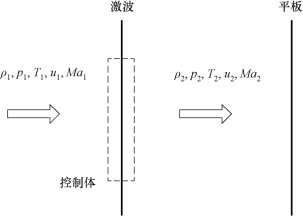
图3.13　正激波

由动量守恒定律，有

即

而能量守恒方程为

代入理想气体状态方程得到

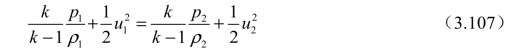
此外，根据状态方程本身可以得到

根据激波前后流动参数满足的基本方程，可以进一步推导二者的关系式。

1. 压强比 p 2/p1

将动量方程（3.105）变形为

由质量方程（3.103）可得

将式（3.110）与理想气体状态方程代入式（3.109）可得

用同样的方法，我们将质量方程与能量方程联立整理后可以得到

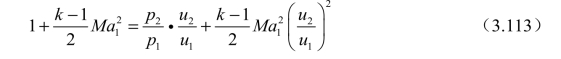
将式（3.112）代入式（3.113）后得

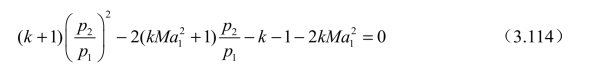
求解后可得

将式（3.116）代入式（3.112）可得

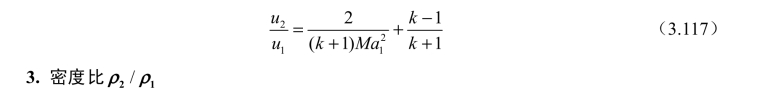
将式（3.117）代入式（3.110）可得

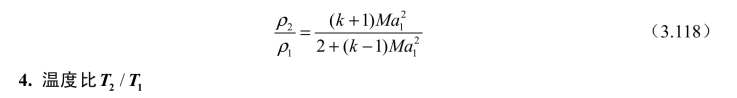
将式（3.115）与式（3.118）代入式（3.108）可得(www.daowen.com)

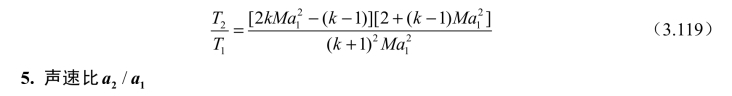
由声速与温度之间的关系可得

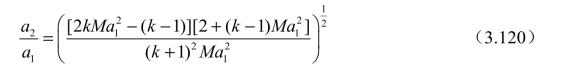
6. 激波前后马赫数关系

由式（3.117）与式（3.120）可得

即正激波波后必然为亚声速流动。

7. 总压比p0 2/p01

由于

代入波前与波后各自的等熵关系式，以及波前波后压强关系可得

由式（3.106）可得

即

式（3.128）说明激波前后总温与总焓是不变的。根据等熵关系式，可以进一步得到

即激波前后临界温度与临界声速不变。

9. 普朗特关系式

根据能量方程，有

代入理想气体状态方程与临界状态的定义可得

即

结合速度比公式（3.117）可得

此即普朗特关系式。式（3.134）说明，由于来流是超声速的，因此正激波后的流动必然是亚声速的。

10. 朗金−雨贡纽关系式

将式（3.116）、式（3.118）与式（3.119）联立，消去其中的M1a 可得

式（3.135）～式（3.137）即朗金−雨贡纽（Rankine-Hugoniot，RH）关系式。可以看出，激波前后的压强比、密度比和温度比是一一对应的。