实际工程中，我们面对的都是有限偏转角的流动问题，其中涉及的流动主要为普朗特−迈耶尔流动（Prandtl-Meyer flow）。所谓普朗特−迈耶尔流动，即平面、定常、超声速气流沿光滑凸（或凹）壁面偏转的等熵流动，如图3.11 所示。超声速气流流过连续偏转的壁面并且始终保持流动方向与壁面平行，显然，对于凸壁面，在偏转的过程中流动面积增大，超声速气流经过膨胀波后逐渐膨胀加速；对于凹壁面，在偏转过程中流动面积减小，超声速气流经过压缩波后逐渐压缩减速。

图3.11　凸、凹壁面普朗特−迈耶尔流动

（a）凸壁面；（b）凹壁面

对于扇形膨胀波，具有有限转角的流动偏转可以看作是经过无数个微小偏转的逐步累积。也就是说，图3.11（a）中的流动偏转与图3.12（a）是等效的，在气流的拐点处形成了扇形膨胀波，整个流动过程仍然可以视作等熵流动。因此，我们只需要知道扇形膨胀波后的马赫数，就可以通过等熵关系式得到偏转前与偏转后流动参数之间的关系。根据马赫数Ma 的定义，可以得到

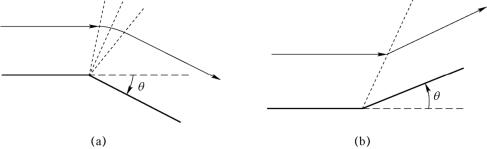
图3.12　扇形膨胀波与强压缩波的产生

（a）凸转角；（b）凹转角

根据等熵关系式，有

微分后得

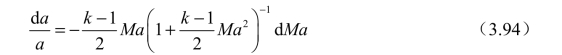
将式（3.94）代入式（3.92）得

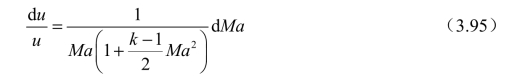
将式（3.95）代入式（3.90）可得(www.daowen.com)

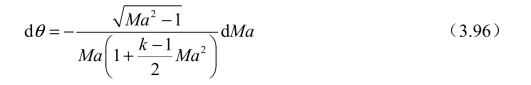
对式（3.96）积分可得

其中，C 为积分常数。定义普朗特−迈耶尔函数为

则有

假设来流马赫数为M1a ，初始（initial）偏转角θ 1 =0 ，则

即

式（3.101）适用于左伸膨胀波，对于右伸膨胀波，有

由式（3.101）与式（3.102）可知，对于普朗特−迈耶尔流动，在已知来流马赫数与偏转角度的前提下，偏转后的马赫数是确定的，进而可以获得偏转前后流场参数之间的关系。

对于凹偏转，如果整个压缩过程是等熵的，仍可按照上述分析过程得到相似的结论。然而，实际情况下，无数个弱压缩波会汇聚成一道强压缩波［图3.12（b）］，使得气流流过压缩波的过程不再是热力学平衡过程。换句话说，强压缩波对应的是非等熵流动。此时，上述分析不再适用，我们需要对强压缩波单独进行分析。