如前所述，当外界压强与燃烧室总压满足一定条件时，在喷管扩张段会产生激波。实际上，超声速燃气从喷管喷出形成射流后，在射流内部同样存在着交替出现的激波与膨胀波。那么，究竟什么是激波？什么是膨胀波？它们因何而产生，又具有哪些特性呢？

首先，我们来认识一下马赫波。所谓马赫波，指的就是我们之前在定义声速时所说的扰动源产生的微小扰动。因此马赫波的传播速度即声速。当扰动源静止（u=0 ）时，马赫波的波阵面为一个个同心球，如图3.9（a）所示。当扰动源相对于周围介质以亚声速（u ＜a ）运动时，根据多普勒效应，波阵面不再同心，每个球形波阵面的球心为该马赫波产生时扰动源的位置，如图3.9（b）所示。当扰动源继续加速达到声速，即u =a ，如图3.9（c）所示，此时所有波阵面在前缘点（扰动源当前位置）处相切，并且所有的微弱扰动波都无法向前超过前缘点。也就是说，此时扰动源相对于周围介质的运动速度与微弱扰动在介质中的传播速度一致，前缘相切点所在的与扰动源运动方向垂直的平面将扰动隔绝在了空间中的一侧。而当扰动源继续加速到超声速状态（u ＞a ），如图3.9（d）所示，此时扰动源的运动速度超过了微弱扰动的传播速度，使得多个球形波阵面包络形成一个锥面（扰动源位于锥顶），锥面内的任何微弱扰动都无法穿过锥面向外传播。这一锥面称为马赫锥。该锥面的半锥角μ 称为马赫角。在可压缩流动中，马赫角是一个重要的概念。从图3.9（d）中的几何关系可以得出

图3.9　马赫波的传播

（a）u=0 ；（b）u ＜a ；（c）u =a ；（d）u ＞a

代入马赫数Ma 的定义后得

或

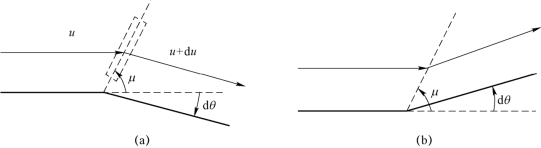
那么，什么样的微小扰动可以在超声速流动中产生马赫锥呢？比较典型的例子是二维流动中的微小偏转。如图3.10 所示，超声速来流沿壁面流动并随壁面产生了微小偏转，偏转的角度为微分量dθ 。对于凸转角，dθ ＜0 ，形成的马赫波为弱膨胀波；对于凹转角，dθ ＞0 ，形成的马赫波为弱压缩波。显然，对于二维问题，马赫锥退化为一道与来流方向存在一定夹角的平面马赫波，夹角大小为马赫角μ。选取图3.10（a）所示的横跨马赫波的控制体，其中控制体的厚度趋近于0。由于控制体内的气流在马赫波切向方向上受力平衡，根据动量守恒，马赫波前后切向速度分量不变，即

(www.daowen.com)

图3.10　微小偏转角流动（左伸）

（a）凸转角；（b）凹转角

整理后得

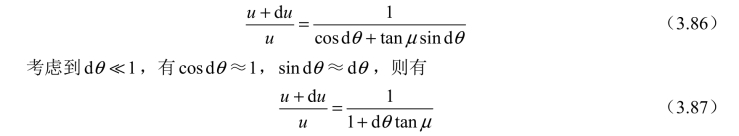
整理并忽略二阶小量后得到

由式（3.83）得

代入式（3.88）后得

式（3.90）即为左伸马赫波对应的来流马赫数与流动偏转角之间的关系。所谓左伸，指的是马赫波伸展方向是相对于来流偏向左的。对于右伸马赫波，式（3.90）变为

具体推导过程留给读者自行练习。显然，式（3.90）与式（3.91）成立的前提是Ma＞1 ，即形成马赫波的来流必须是超声速的。