目前为止，我们介绍了拉瓦尔喷管内燃气的流动规律，并建立了喷管内任意截面流动参数与燃烧室总温、总压等参数之间的关系。那么，掌握这些关系对于我们解决工程问题有什么帮助呢？

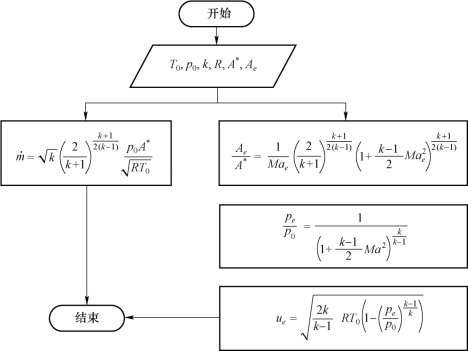
拉瓦尔喷管设计的正问题，即已知火箭发动机燃烧室内的参数以及拉瓦尔喷管的型面，求在设计状态下拉瓦尔喷管燃气流量、出口速度，乃至整个喷管内的燃气流动参数分布。换句话说，正问题就是我们在已经知道火箭发动机的具体设计参数的情况下，通过计算预估其理想状态下的性能指标。正问题通常用于对发动机设计指标（如推力）进行初步验证。对于喷管流量，在已知其燃烧室总温、总压的情况下，可以直接通过式（3.80）计算得出。出口速度需要根据式（3.68）计算，显然，式中涉及压强比pe /p0 。因此首先需要通过喷管出口与喉部截面面积比Ae /A* ，计算出喷管出口的马赫数Ma e，然后根据等熵流动关系式（3.57）求出pe /p0 并代入式（3.68），进而求得出口速度 u e。拉瓦尔喷管正问题求解流程如图3.8 所示。

(www.daowen.com)

图3.8　拉瓦尔喷管正问题求解流程

拉瓦尔喷管正问题求解首先需要获取火箭发动机燃烧室内的各种参数，包括总温 T0 、总压 p0 等。这些参数一般通过试验测量直接获取，或者根据推进剂燃烧的热力学平衡计算得出。推进剂燃烧的热力学平衡控制方程包括质量守恒方程、能量守恒方程（热力学第一定律）以及化学平衡方程（热力学第二定律）。选定 T0 、p 0后，建立由质量守恒方程和化学平衡方程构成的非线性方程组，选取合适的数值求解方法，如线性化、牛顿迭代、同伦算法等对非线性方程组进行求解，得出满足当前总温、总压下，质量守恒与化学反应平衡的燃烧产物质量分数。根据该质量分数，计算此时能量守恒方程的残差，并以此修正 T0 、p 0，直至满足全部控制方程。具体的求解过程可以参考火箭发动机相关书籍，此处不做详细介绍。计算得出的 T0 、p0即可作为拉瓦尔喷管正问题的输入条件，并且可以通过相应的燃气组分计算燃气混合物的比热比k 以及气体常数R。这样，结合喷管的具体型面参数，就可以顺利完成正问题求解。

与正问题不同，拉瓦尔喷管的反问题是通过已知的燃气流量m˙与出口速度 u e，反推出发动机燃烧室参数甚至喷管的型面特征尺寸。反问题同样具有非常高的工程实用价值。例如，给定发动机的推力设计指标，如何对燃烧室内的总温、总压设计值做出合理的初步预估？在发动机燃烧室性能不便获取的情况下，如何根据燃气流量与喷管出口流速等参数，反推出燃烧室内的大致参数？这些都是工程中经常遇到的实际问题。反问题求解中涉及的方程与正问题基本一致，区别仅在于方程中的已知量与未知量不同，因此不再赘述。