通过上面的推导，我们得到了无黏、绝热传导条件下的准一维定常流动控制方程组：式（3.2）、式（3.6）与式（3.12）。接下来，我们需要将得到的方程用于分析喷管内燃气流动。根据我们的直观感受，喷管的截面面积A 对喷管内流动的影响较大。不同喷管出口截面面积对应不同的速度，即对应不同的推力。为此，我们首先来分析喷管截面面积与速度之间的关系。对于不可压流体有

此时速度u 随着流动面积A 增大而减小。然而，燃气在喷管中的流动属于可压缩流动，针对不可压流动得到的这一关系并没有很强的指导意义。可压缩流动的速度u 不仅与流动面积A有关，还与流体密度ρ 有关。可见，可压缩流动的速度随流动面积的变化规律并不像想象中那样简单。想要得到可压缩流动参数随截面面积变化的规律，我们需要针对可压缩流动的特点引入一些新的概念。

生活中存在着各种各样的声音：鸟儿的鸣叫、寺院的钟声、飞机起飞的轰鸣等。这些声音是如何产生的呢？以寺院的钟声为例，我们敲钟给钟一个扰动，这个扰动对应着钟各个位置应力、密度和速度的变化。同时，钟又会将这个扰动传递给周围的空气，并借由空气传到人们的耳朵里。声音本质上是一种机械波，与传播介质的可压缩性有关。为了定量描述声波传播的快慢，我们定义声速a 为声波相对于传播介质的速度，即微小扰动在静止介质中传播的速度。下面，选用一个简单的模型来分析声波的传播速度。

图3.4 显示了等截面管道中，声波在可压缩气体介质中的传播过程。以管道为参考系，声波在管道中从左向右匀速传播。声波传播经过的区域，对应的流动参数会发生改变。我们关注的重点在于声波传播的速度与波前与波后流动参数之间的关系。为此，我们以声波为参考系，并选取图3.5 所示的控制体。我们使得选取的控制体的左右两端无限趋近于声波位置，这样就可以忽略壁面对控制体内流体的传热与剪切力。根据质量守恒定律，我们可以得到

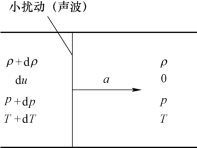
图3.4　声波传播

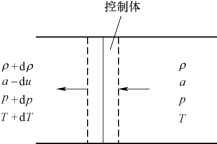
图3.5　控制体的选取

展开并忽略二阶小量：

由动量守恒定律可得

(www.daowen.com)

整理后可得

结合式（3.20）与式（3.22），消去du，最后整理得到

式（3.23）即为可压缩气体中声速的表达式。

如前所述，声波的传播与介质的可压缩性有关。为了更为明确地揭示这一关系，我们将式（2.3）与式（3.23）联立可得

或

由式（3.24）与式（3.25）可以看出，密度和声速越大的介质，其可压缩性越弱；相反，密度越小、可压缩性越弱的介质，其声速越大。这一结论与我们日常生活中的经验是一致的，例如，声音在钢铁中的传播速度就远大于空气。

对于处于静止状态的气体，声速能够很好地衡量其可压缩性。而对于流动的可压缩气体，其密度ρ 与其流动状态有关，即不同的流动状态下，气体的可压缩性是不同的。为了更好地衡量流动气体的可压缩性，我们引入一个新的无量纲参数——马赫数Ma，定义为

根据Ma 不同，可以将流体的流动划分为亚声速流动（Ma ＜1 ）与超声速流动（Ma＞1 ）。