动量守恒定律也是任何流动系统都必须满足的基本定律。对于宏观物体运动，动量守恒定律与牛顿第二定律是一致的。对于流体动力学问题，该定律可表述为：流体团动量对时间的变化率等于流体团所受合外力。首先，我们推导积分形式的动量守恒方程。取某一流体团为研究对象，假设该流体团刚好与某一控制体重合，根据定义，有

其中，u i 为速度V 的第i 个分量； iF 为合外力的第i 个分量。下面我们来分析一下流体团所受外力都有哪些。首先，我们根据力的作用方式，将合外力分为表面力与体积力。顾名思义，表面力即作用在流体团表面的力，包括压力、黏性力；体积力即作用在整个流体团体积上的力，包括重力、惯性力等。由于体积力相对简单，因此后面的推导过程中忽略体积力，仅考虑表面力的影响。

在i 方向上，流体团所受压力为

其中，p 为流体团表面压强；dS 为流体团表面面积矢量微元； in 为i 方向的单位向量。

黏性力的形式略微复杂，为

其中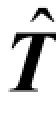， 为黏性力张量。黏性力张量是一个二阶张量，数学上表示为一个方矩阵，矩阵中的每一个分量表示一个黏性应力，记为 ijτ ，其中i 表示黏性应力的作用面法线方向；j 表示黏性应力的方向。在三维笛卡儿坐标系下，黏性力张量可以表示为

对式（2.20）和式（2.21）使用高斯定理，最终可以得到

下面来推导微分形式的动量守恒方程。选择某一流体微团作为研究对象，假设该流体微团刚好与某一微元控制体重合，则有(www.daowen.com)

由于流体微团质量不随时间变化，因此式（2.24）可以化为

实际上，式（2.25）已经是微分形式的动量守恒方程。然而，通过观察不难发现，式中既有全导数又有偏导数，即方程左右两端描述方法上存在分歧。为了统一形式，对方程左端代入式（2.7）后得

再次利用求导乘法法则，可以得到

根据式（2.15），方程右端最后一项为0（质量守恒），则有

最后，我们可以得到

式（2.29）即统一形式后的微分形式动量守恒方程。